Kapitola 14 Podpůrné materiály pro diplomovou práci

V této poslední kapitole jsou uvedeny zdrojové kódy pro vygenerování grafů a dalších případných materiálů, které jsou použity v diplomové práci. Jedná se především o ilustrativní grafy určitých vlastností a fenoménů spojených s funkcionálními daty.

Kapitola je členěna do sekcí, které odpovídají jednotlivým kapitolám v diplomové práci. Všechny grafy jsou vytvořeny pomocí balíčku ggplot2, který poskytuje celou řadu grafických funkcionalit, pomocí kterých jsme (alespoň subjektivně) schopni dosáhnout podstatně lépe a profesionálněji vypadajících grafických výstupů v porovnání s klasickou grafikou v R.

Všechny grafy jsou uloženy pomocí funkce ggsave() ve formátu pdf nebo tikz, který umožňuje lepší kombinaci grafiky a symbolů v \(\LaTeX\)u.

Code

# nacteme potrebne balicky 
library(fda)
library(ggplot2)
library(dplyr)
library(tidyr)
library(ddalpha)
library(tidyverse)
library(patchwork)
library(tikzDevice)

set.seed(42)
options(tz = "UTC")

# nacteni dat
data <- read.delim2('phoneme.txt', header = T, sep = ',')

# zmenime dve promenne na typ factor
data <- data |> 
  mutate(g = factor(g),
         speaker = factor(speaker))

# numericke promenne prevedeme opravdu na numericke
data[, 2:257] <- as.numeric(data[, 2:257] |> as.matrix())

tr_vs_test <- str_split(data$speaker, '\\.') |> unlist()
tr_vs_test <- tr_vs_test[seq(1, length(tr_vs_test), by = 4)]
data$train <- ifelse(tr_vs_test == 'train', TRUE, FALSE)

# vybrane fonemy ke klasifikaci
phoneme_subset <- c('aa', 'ao')

# testovaci a trenovaci data
data_train <- data |> filter(train) |> filter(g %in% phoneme_subset)
data_test <- data |> filter(!train) |> filter(g %in% phoneme_subset)

# odstranime sloupce, ktere nenesou informaci o frekvenci a 
# transponujeme tak, aby ve sloupcich byly jednotlive zaznamy
X_train <- data_train[, -c(1, 258, 259, 260)] |> t()
X_test <- data_test[, -c(1, 258, 259, 260)] |> t()

# prejmenujeme radky a sloupce
rownames(X_train) <- 1:256
colnames(X_train) <- paste0('train', data_train$row.names)
rownames(X_test) <- 1:256
colnames(X_test) <- paste0('test', data_test$row.names)

# definujeme vektor fonemu
y_train <- data_train[, 258] |> factor(levels = phoneme_subset)
y_test <- data_test[, 258] |> factor(levels = phoneme_subset)
y <- c(y_train, y_test)

14.1 Materiály pro Kapitolu 1

V této sekci uvedeme podpůrné grafy pro první kapitolu diplomové práce.

14.1.1 Funkcionální průměr

Pro data phoneme spočítáme průměrný průběh log-periodogramů.

Code

t <- 1:256
rangeval <- range(t)
breaks <- t
norder <- 4

bbasis <- create.bspline.basis(rangeval = rangeval, 
                               norder = norder, 
                               breaks = breaks)

curv.Lfd <- int2Lfd(2) # penalizujeme 2. derivaci

# spojeni pozorovani do jedne matice
XX <- cbind(X_train, X_test) |> as.matrix()
XXaa <- XX[, y == phoneme_subset[1]]

lambda.vect <- 10^seq(from = 1, to = 3, length.out = 35) # vektor lambd
gcv <- rep(NA, length = length(lambda.vect)) # prazdny vektor pro ulozebi GCV

for(index in 1:length(lambda.vect)) {
  curv.Fdpar <- fdPar(bbasis, curv.Lfd, lambda.vect[index])
  BSmooth <- smooth.basis(t, XX, curv.Fdpar) # vyhlazeni
  gcv[index] <- mean(BSmooth$gcv) # prumer pres vsechny pozorovane krivky
}

GCV <- data.frame(
  lambda = round(log10(lambda.vect), 3),
  GCV = gcv
)

# najdeme hodnotu minima
lambda.opt <- lambda.vect[which.min(gcv)]

curv.fdPar <- fdPar(bbasis, curv.Lfd, lambda.opt)
BSmooth <- smooth.basis(t, XX, curv.fdPar)
XXfd <- BSmooth$fd

fdobjSmootheval <- eval.fd(fdobj = XXfd, evalarg = t)

## pouze pro aa
lambda.vect <- 10^seq(from = 1, to = 3, length.out = 35) # vektor lambd
gcv <- rep(NA, length = length(lambda.vect)) # prazdny vektor pro ulozebi GCV

for(index in 1:length(lambda.vect)) {
  curv.Fdpar <- fdPar(bbasis, curv.Lfd, lambda.vect[index])
  BSmoothaa <- smooth.basis(t, XXaa, curv.Fdpar) # vyhlazeni
  gcv[index] <- mean(BSmoothaa$gcv) # prumer pres vsechny pozorovane krivky
}

GCV <- data.frame(
  lambda = round(log10(lambda.vect), 3),
  GCV = gcv
)

# najdeme hodnotu minima
lambda.opt <- lambda.vect[which.min(gcv)]

curv.fdPar <- fdPar(bbasis, curv.Lfd, lambda.opt)
BSmoothaa <- smooth.basis(t, XXaa, curv.fdPar)
XXfdaa <- BSmoothaa$fd

fdobjSmoothevalaa <- eval.fd(fdobj = XXfdaa, evalarg = t)

# prumer 
meanfd <- mean.fd(XXfdaa)
fdmean <- eval.fd(fdobj = meanfd, evalarg = t)

Code

n <- dim(XX)[2]
DFsmooth <- data.frame(
  t = rep(t, n),
  time = factor(rep(1:n, each = length(t))),
  Smooth = c(fdobjSmootheval),
  Phoneme = rep(y, each = length(t))) |>
  filter(Phoneme == 'aa')

DFmean <- data.frame(
  t = rep(t, 2),
  Mean = c(fdmean, fdmean),
  Phoneme = factor(rep(phoneme_subset, each = length(t)),
                 levels = levels(y))
) |> filter(Phoneme == 'aa')

# tikz(file = "figures/DP_kap1_mean.tex", width = 4.2, height = 3.5)

DFsmooth |> 
  filter(time %in% as.character(1:100)) |>
  ggplot(aes(x = t, y = Smooth)) + 
  geom_line(aes(group = time), linewidth = 0.2, colour = 'deepskyblue2',
            alpha = 0.6) +
  theme_bw() +
  labs(x = 'Frekvence',
       y = 'Log-periodogram',
       colour = 'Phoneme') +
  scale_colour_discrete(labels = phoneme_subset) + 
  geom_line(data = DFmean, aes(x = t, y = Mean, 
                               group = Phoneme), 
            linewidth = 1, linetype = 'solid', colour = 'grey2') + 
  theme(legend.position = 'none')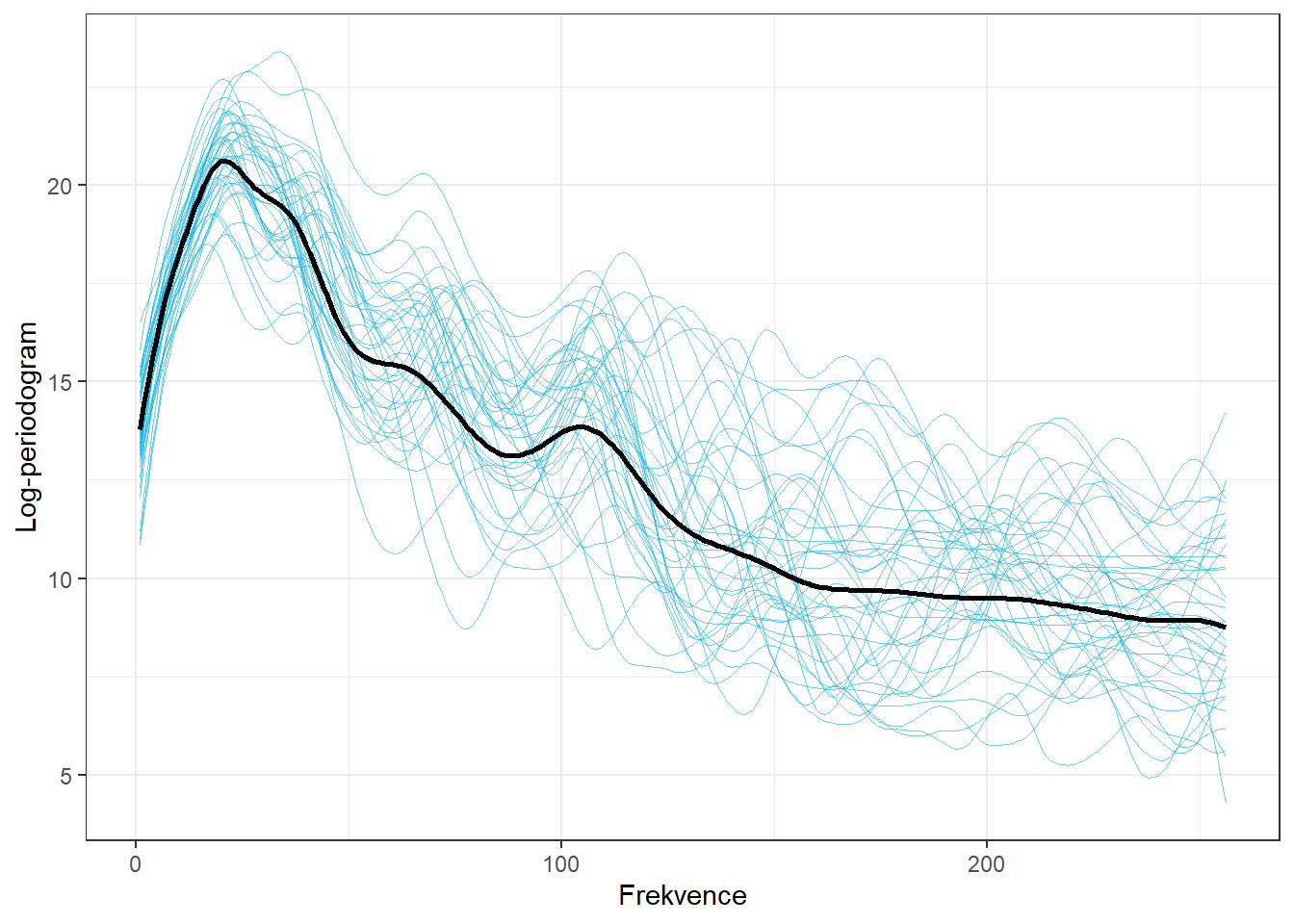

Obrázek 1.1: Vykreslení prvních 100 vyhlazených pozorovaných křivek. Černou čarou je zakreslen průměr.

Code

# dev.off()
# ggsave("figures/DP_kap1_mean.pdf", width = 6, height = 5)

14.1.2 Variance

Pro data phoneme spočítáme průběh varianční funkce.

Code

varfd <- var.fd(XXfdaa)
fdvar <- eval.bifd(t, t, varfd)

Code

dfs <- data.frame(
  time = t, 
  value = c(fdobjSmoothevalaa))
df <- data.frame(dfs, fdmean = fdmean, fdvar = diag(fdvar))

# tikz(file = "figures/DP_kap1_variance.tex", width = 6, height = 5)
# df <- df[seq(1, length(df$time), length = 1001), ]

ggplot(data = df, aes(x = time, y = fdvar)) +
  geom_line(color = 'deepskyblue2', linewidth = 0.8) +
  labs(x = 'Frekvence',
       y = 'Variance',
       colour = 'Phoneme') +
  theme_bw()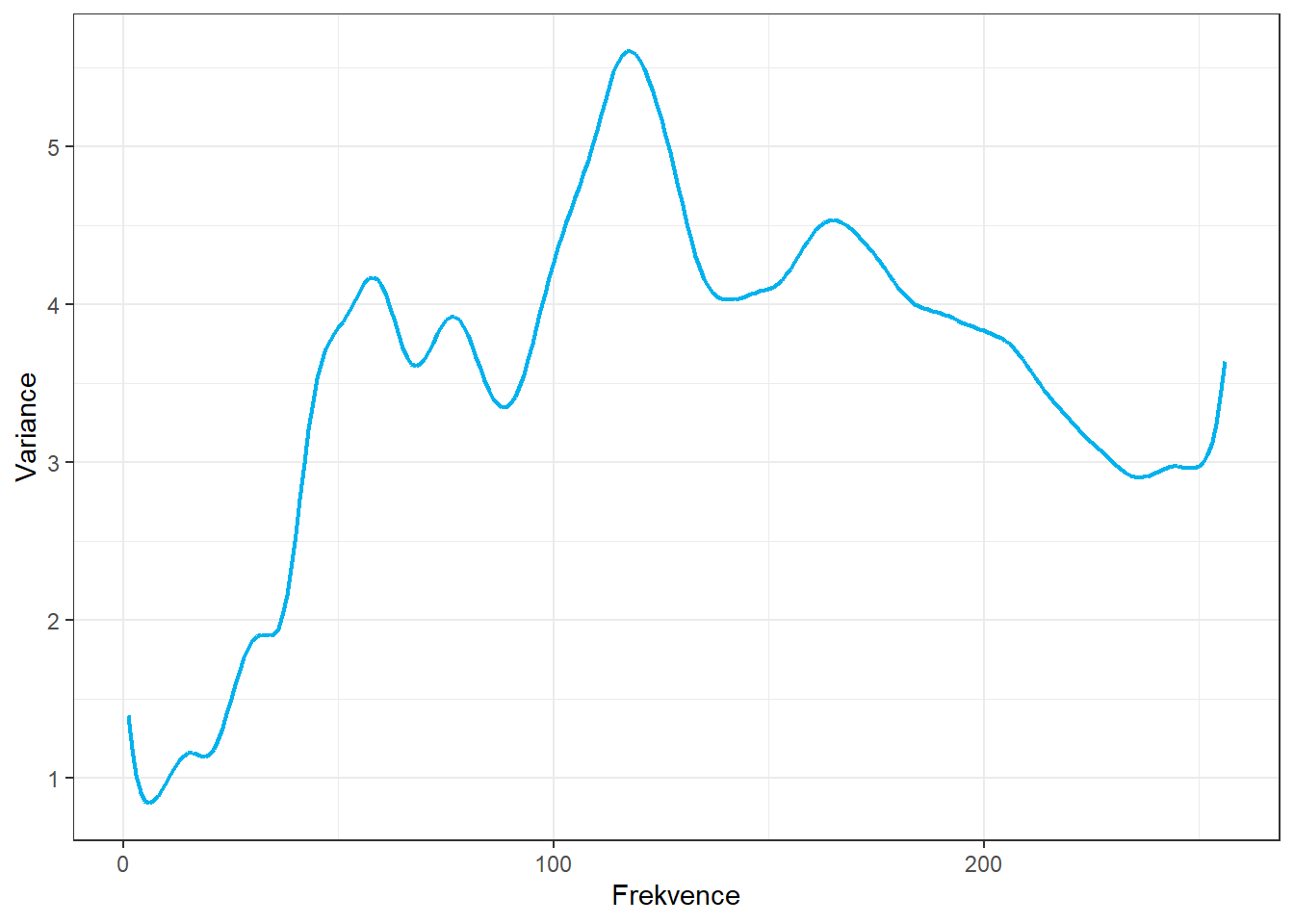

Obrázek 3.1: Varianční funkce.

Code

 # dev.off()
# ggsave("figures/DP_kap1_variance.tex", width = 4.2, height = 3.5, device = tikz)

14.1.3 Kovariance a Korelace

Pro data phoneme spočítáme kovarianční a korelační funkce.

Code

fdcor <- cor.fd(t, XXfdaa) 

df <- merge(t, t)
df <- data.frame(df, fdcov = c(fdvar), fdcor = c(fdcor))
df <- df[seq(1, length(df$x), length = 68001), ]

# tikz(file = "figures/DP_kap1_cov.tex", width = 4, height = 4)

p1 <- ggplot(data = df, aes (x, y, z = fdcov)) +
  geom_raster(aes(fill = fdcov)) +
  geom_contour(colour = "white") +
  labs(x = 'Frekvence',
       y = 'Frekvence',
       fill = 'Kovariance') +
  coord_fixed(ratio = 1) + 
  theme_bw() + 
  theme(legend.position = 'bottom') + 
  scale_y_continuous(expand = c(0,0) + 0.01) + 
  scale_x_continuous(expand = c(0,0) + 0.01)
p1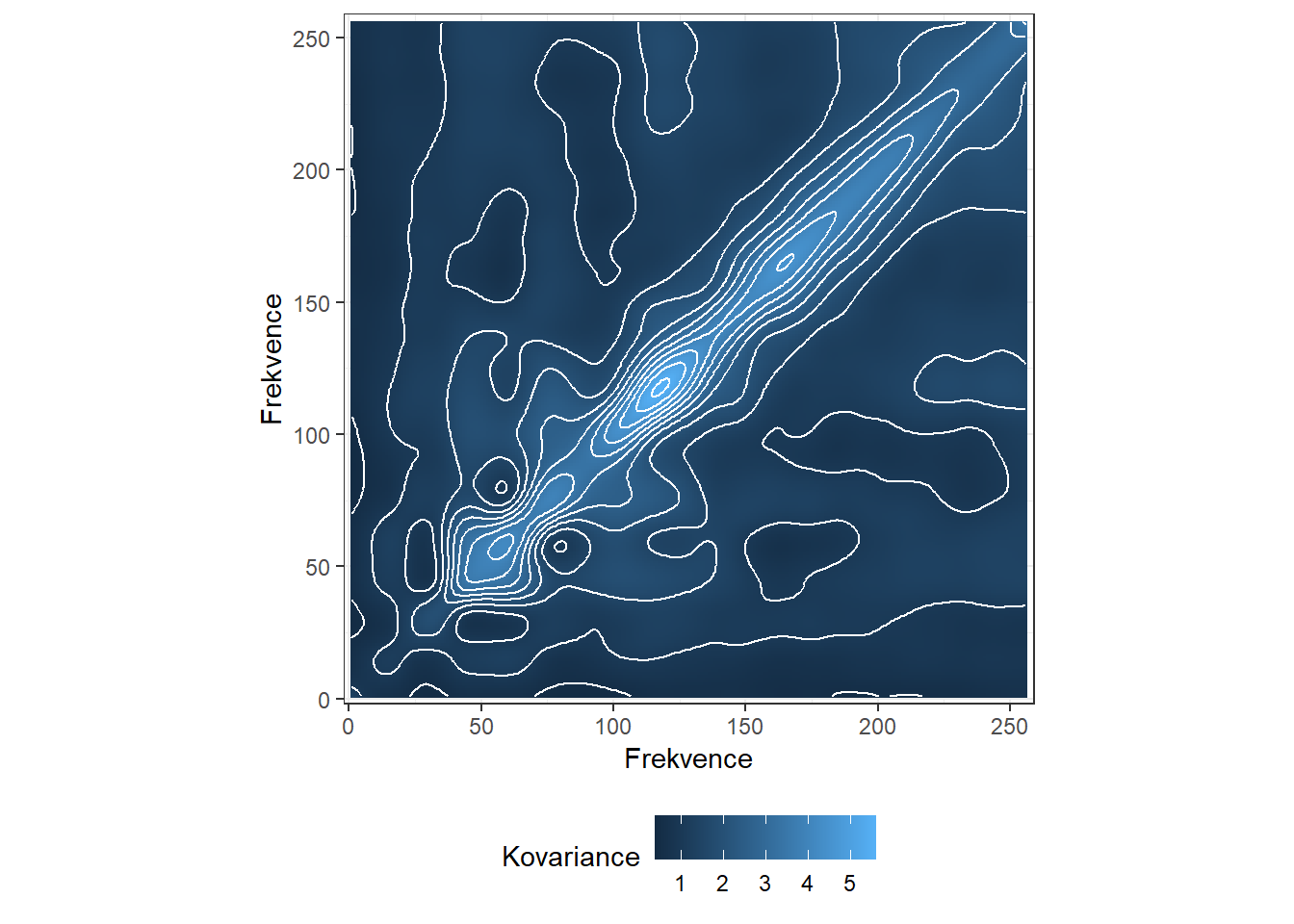

Code

# dev.off()
# ggsave("figures/DP_kap1_cov.tex", width = 6, height = 6, device = tikz)
# tikz(file = "figures/DP_kap1_cor.tex", width = 4, height = 4)
p2 <- ggplot(data = df, aes (x, y, z = fdcor)) +
  geom_raster(aes(fill = fdcor)) +
  geom_contour(colour = "white") +
  labs(x = 'Frekvence',
       y = 'Frekvence',
       fill = 'Korelace') +
  coord_fixed(ratio = 1) + 
  theme_bw() + 
  theme(legend.position = 'bottom') + 
  scale_y_continuous(expand = c(0,0) + 0.01) + 
  scale_x_continuous(expand = c(0,0) + 0.01)
p2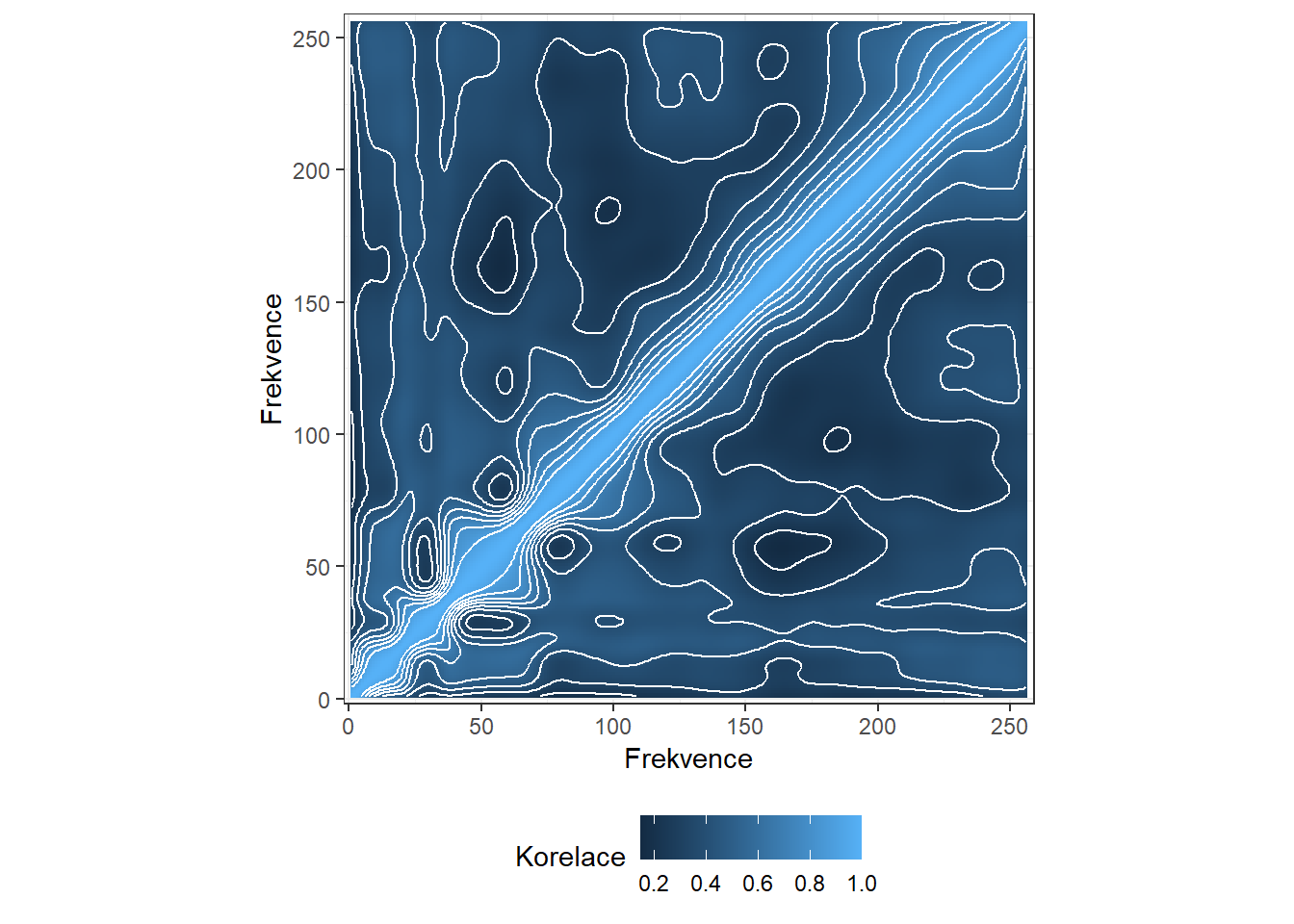

Code

# dev.off()
# ggsave("figures/DP_kap1_cor.tex", width = 6, height = 6, device = tikz)

14.1.4 B-splinová báze

Podívejme se na princip, jak se pomocí splinové báze dostaneme od diskrétních naměřených hodnot k funkcionálním datům.

Uvažujme pro přehlednost opět data phoneme a pouze malý počet bázových funkcí. Uvedeme tři obrázky, jeden se znázorněnými bázovými funkcemi, druhý s bázovými funkcemi přenásobenými vypočtenou hodnotou parametru a třetí výslednou křivku poskládanou sečtením jednotlivých přeškálovaných bázových funkcí.

Code

# definice barev 
cols7 <- c("#12DEE8", "#4ECBF3", "#127DE8", "#4C3CD3", "#4E65F3", "#4E9EF3", "#081D58")
cols5 <- c("#12DEE8",  "#1D89BC", "#4E9EF3", "#4C3CD3", "#081D58")

14.1.4.1 pro `norder = 2`

Code

df <- data.frame(x = 1:256, y = data[5, 2:257] |> c() |> unlist())
breaks <- quantile(df$x, probs = seq(0.1, 0.9, by = 0.2))
norder <- 2
rangeval <- range(df$x)

bbasis <- create.bspline.basis(rangeval, norder = norder, breaks = breaks)
BSmooth <- smooth.basis(df$x, df$y, bbasis)

Code

fdBSmootheval <- eval.fd(fdobj = BSmooth$fd, evalarg = df$x)
fdB <- eval.basis(basisobj = bbasis, evalarg = df$x)

basisdf1 <-  data.frame(bs = c(fdB), 
                        x = df$x, 
                        basis = rep(colnames(fdB), each = length(df$x)))
ebchan <- fdB * matrix(rep(BSmooth$fd$coefs, each = length(df$x)),
                       nrow = length(df$x))
basisdf2 <-  data.frame(bs = c(ebchan), 
                        x = df$x, 
                        basis = rep(colnames(fdB), each = length(df$x)))

library(RColorBrewer)

# tikz(file = "figures/DP_kap1_Bbasis_norder2.tex", width = 9, height = 3)

# samotna baze
p1 <- ggplot(data = basisdf1, aes(x = x, y = bs * 10, colour = basis)) +
  geom_vline(xintercept = breaks, linetype = "dotted", linewidth = 0.1, colour = 'grey2') +
  geom_line() +
  labs(x = 'Frekvence',
       y = 'B-splajnová báze',
       colour = 'Foném') +
  theme_classic() + 
  guides(colour = FALSE) +
  ylim(c(0, 22)) + 
  # scale_color_brewer(palette = 'Blues') +
  # scale_color_manual(values = colorRampPalette(brewer.pal(9, "YlGnBu"))(12)[c(6,8,9,10,12)])
  scale_color_manual(values = cols5)

# prenasobena koeficienty
p2 <- ggplot(data = basisdf2, aes(x = x, y = bs, colour = basis)) +
  geom_vline(xintercept = breaks, linetype = "dotted", linewidth = 0.1, colour = 'grey2') +
  geom_line() + 
  labs(x = 'Frekvence',
       y = 'B-splajnová báze (škálovaná)',
       colour = 'Foném') +
  theme_classic() + 
  guides(colour = FALSE) + 
  ylim(c(0, 22)) + 
  # scale_color_brewer()
  # scale_color_manual(values = colorRampPalette(brewer.pal(9, "YlGnBu"))(12)[c(6,8,9,10,12)])
  scale_color_manual(values = cols5)

# vyhlazena data
p3 <- ggplot(data = df, aes(x, y)) + 
  geom_vline(xintercept = breaks, linetype = "dotted", linewidth = 0.1, colour = 'grey2') +
  geom_point(colour = 'deepskyblue2', size = 0.8, alpha = 0.75) +
  geom_line(aes(y = fdBSmootheval)) +
  theme_classic() + 
  #guides (colour = FALSE) + 
  ylim(c(0, 22)) + 
  labs(x = 'Frekvence',
       y = 'Log-periodogram',
       colour = 'Foném')

(p1 | p2 | p3)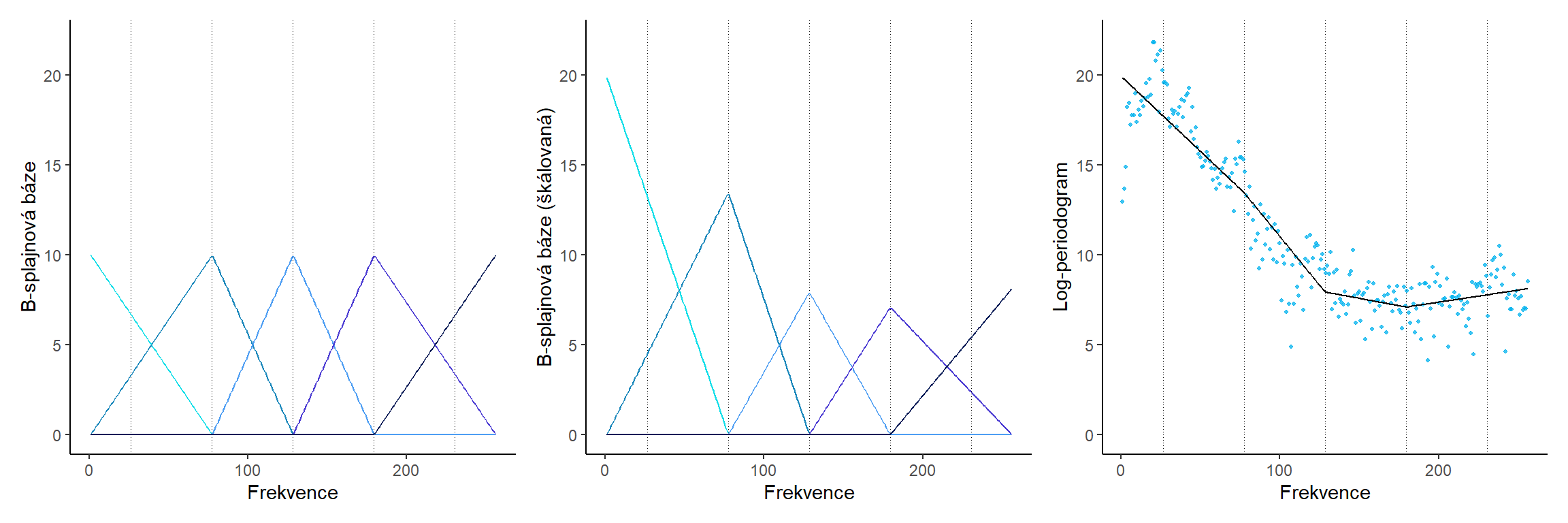

Obrázek 1.3: B-spliny.

Code

# dev.off()
# ggsave('figures/DP_kap1_Bbasis_norder2.tex', device = tikz)

14.1.4.2 pro `norder = 4`

Code

df <- data.frame(x = 1:256, y = data[5, 2:257] |> c() |> unlist())
breaks <- quantile(df$x, probs = seq(0.1, 0.9, by = 0.2))
norder <- 4
rangeval <- range(df$x)

bbasis <- create.bspline.basis (rangeval, norder = norder, breaks = breaks)
BSmooth <- smooth.basis(df$x, df$y, bbasis)

Code

fdBSmootheval <- eval.fd(fdobj = BSmooth$fd, evalarg = df$x)
fdB <- eval.basis(basisobj = bbasis, evalarg = df$x)

basisdf1 <-  data.frame(bs = c(fdB), 
                        x = df$x, 
                        basis = rep(colnames(fdB), each = length(df$x)))
ebchan <- fdB * matrix(rep(BSmooth$fd$coefs, each = length(df$x)),
                       nrow = length(df$x))
basisdf2 <-  data.frame(bs = c(ebchan), 
                        x = df$x, 
                        basis = rep(colnames(fdB), each = length(df$x)))

# tikz(file = "figures/DP_kap1_Bbasis_norder4.tex", width = 9, height = 3)

# samotna baze
p1 <- ggplot(data = basisdf1, aes(x = x, y = bs * 10, colour = basis)) +
  geom_vline(xintercept = breaks, linetype = "dotted", linewidth = 0.1, colour = 'grey2') +
  geom_line() +
  labs(x = 'Frekvence',
       y = 'B-splajnová báze',
       colour = 'Foném') +
  theme_classic() + 
  guides(colour = FALSE) +
  ylim(c(0, 22)) + 
  # scale_color_brewer(palette = 'Blues') + 
  # scale_color_manual(values = colorRampPalette(brewer.pal(9, "YlGnBu"))(12)[c(6,8,9,10,12)])
  scale_color_manual(values = cols7)

# prenasobena koeficienty
p2 <- ggplot(data = basisdf2, aes(x = x, y = bs, colour = basis)) +
  geom_vline(xintercept = breaks, linetype = "dotted", linewidth = 0.1, colour = 'grey2') +
  geom_line() + 
  labs(x = 'Frekvence',
       y = 'B-splajnová báze (škálovaná)',
       colour = 'Foném') +
  theme_classic() + 
  guides(colour = FALSE) + 
  ylim(c(0, 22)) + 
  # scale_color_brewer()
  # scale_color_manual(values = colorRampPalette(brewer.pal(9, "YlGnBu"))(12)[c(6,8,9,10,12)])
  scale_color_manual(values = cols7)
  

# vyhlazena data
p3 <- ggplot(data = df, aes(x, y)) + 
  geom_vline(xintercept = breaks, linetype = "dotted", linewidth = 0.1, colour = 'grey2') +
  geom_point(colour = 'deepskyblue2', size = 0.8, alpha = 0.75) +
  geom_line(aes(y = fdBSmootheval)) +
  theme_classic() + 
  #guides (colour = FALSE) + 
  ylim(c(0, 22)) + 
  labs(x = 'Frekvence',
       y = 'Log-periodogram',
       colour = 'Foném')

(p1 | p2 | p3)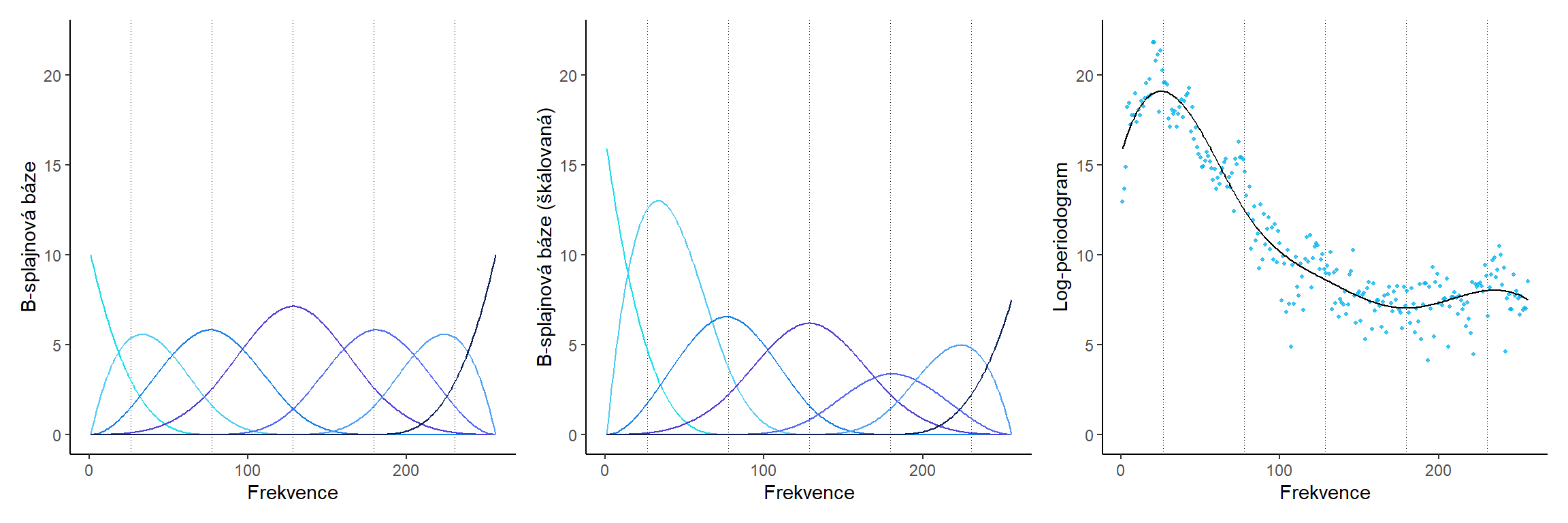

Obrázek 1.5: B-spliny.

Code

# dev.off()
#ggsave('figures/DP_kap1_Bbasis_norder4.pdf')

14.1.5 Fourierova báze

Podívejme se na princip, jak se pomocí Fourierovské báze dostaneme od diskrétních naměřených hodnot k funkcionálním datům.

14.1.5.1 pro `nbasis = 5`

Code

df <- data.frame(x = 1:256, y = data[5, 2:257] |> c() |> unlist())
nbasis <- 5
rangeval <- range(df$x)

fbasis <- create.fourier.basis(rangeval, nbasis = nbasis, period = 256)
FSmooth <- smooth.basis(df$x, df$y, fbasis)

Code

fdBSmootheval <- eval.fd(fdobj = FSmooth$fd, evalarg = df$x)
fdF <- eval.basis(basisobj = fbasis, evalarg = df$x)

basisdf1 <-  data.frame(bs = c(fdF), 
                        x = df$x, 
                        basis = rep(colnames(fdF), each = length(df$x)))
ebchan <- fdF * matrix(rep(FSmooth$fd$coefs, each = length(df$x)),
                       nrow = length(df$x))
basisdf2 <-  data.frame(bs = c(ebchan), 
                        x = df$x, 
                        basis = rep(colnames(fdF), each = length(df$x)))

# tikz(file = "figures/DP_kap1_Fbasis_nbasis5.tex", width = 9, height = 3)

# samotna baze
p1 <- ggplot(data = basisdf1, aes(x = x, y = bs, colour = basis)) +
  # geom_vline(xintercept = breaks, linetype = "dotted", linewidth = 0.1, colour = 'grey') +
  geom_line() +
  labs(x = 'Frekvence',
       y = 'Fourierova báze',
       colour = 'Foném') +
  theme_classic() + 
  guides(colour = FALSE) +
  #ylim(c(0, 22)) + 
  # scale_color_brewer(palette = 'Blues')
  scale_color_manual(values = cols5)

# prenasobena koeficienty
p2 <- ggplot(data = basisdf2, aes(x = x, y = bs, colour = basis)) +
  # geom_vline(xintercept = breaks, linetype = "dotted", linewidth = 0.1, colour = 'grey') +
  geom_line() + 
  labs(x = 'Frekvence',
       y = 'Fourierova báze (škálovaná)',
       colour = 'Foném') +
  theme_classic() + 
  guides(colour = FALSE) + 
  #ylim(c(0, 22)) + 
  # scale_color_brewer()
  scale_color_manual(values = cols5)

# vyhlazena data
p3 <- ggplot(data = df, aes(x, y)) + 
  # geom_vline(xintercept = breaks, linetype = "dotted", linewidth = 0.1, colour = 'grey') +
  geom_point(colour = 'deepskyblue2', size = 0.8, alpha = 0.75) +
  geom_line(aes(y = fdBSmootheval)) +
  theme_classic() + 
  #guides (colour = FALSE) + 
  ylim(c(0, 22)) + 
  labs(x = 'Frekvence',
       y = 'Log-periodogram',
       colour = 'Foném')

(p1 | p2 | p3)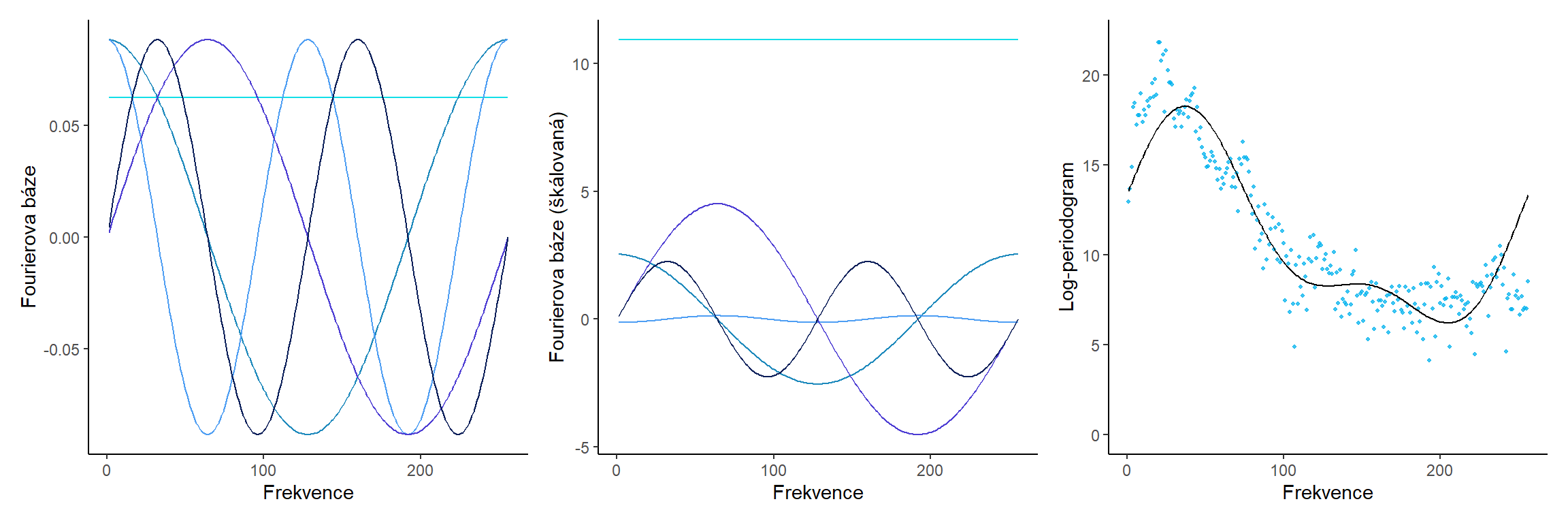

Obrázek 2.2: Fourierova baze.

Code

# dev.off()
#ggsave('figures/DP_kap1_Fbasis_nbasis5.pdf')

14.1.5.2 pro `nbasis = 7`

Code

df <- data.frame(x = 1:256, y = data[5, 2:257] |> c() |> unlist())
nbasis <- 7
rangeval <- range(df$x)

fbasis <- create.fourier.basis(rangeval, nbasis = nbasis, period = 256)
FSmooth <- smooth.basis(df$x, df$y, fbasis)

Code

fdBSmootheval <- eval.fd(fdobj = FSmooth$fd, evalarg = df$x)
fdF <- eval.basis(basisobj = fbasis, evalarg = df$x)

basisdf1 <-  data.frame(bs = c(fdF), 
                        x = df$x, 
                        basis = rep(colnames(fdF), each = length(df$x)))
ebchan <- fdF * matrix(rep(FSmooth$fd$coefs, each = length(df$x)),
                       nrow = length(df$x))
basisdf2 <-  data.frame(bs = c(ebchan), 
                        x = df$x, 
                        basis = rep(colnames(fdF), each = length(df$x)))

# tikz(file = "figures/DP_kap1_Fbasis_nbasis7.tex", width = 12, height = 4)

# samotna baze
p1 <- ggplot(data = basisdf1, aes(x = x, y = bs, colour = basis)) +
  # geom_vline(xintercept = breaks, linetype = "dotted", linewidth = 0.1, colour = 'grey') +
  geom_line() +
  labs(x = 'Frekvence [Hz]',
       y = 'Fourierova báze',
       colour = 'Foném') +
  theme_classic() + 
  guides(colour = FALSE) +
  #ylim(c(0, 22)) + 
  # scale_color_brewer(palette = 'Blues')
  scale_color_manual(values = cols7)

# prenasobena koeficienty
p2 <- ggplot(data = basisdf2, aes(x = x, y = bs, colour = basis)) +
  # geom_vline(xintercept = breaks, linetype = "dotted", linewidth = 0.1, colour = 'grey') +
  geom_line() + 
  labs(x = 'Frekvence [Hz]',
       y = 'Fourierova báze (škálovaná)',
       colour = 'Foném') +
  theme_classic() + 
  guides(colour = FALSE) + 
  #ylim(c(0, 22)) + 
  # scale_color_brewer()
  scale_color_manual(values = cols7)

# vyhlazena data
p3 <- ggplot(data = df, aes(x, y)) + 
  # geom_vline(xintercept = breaks, linetype = "dotted", linewidth = 0.1, colour = 'grey') +
  geom_point(colour = 'deepskyblue2', size = 0.8, alpha = 0.75) +
  geom_line(aes(y = fdBSmootheval)) +
  theme_classic() + 
  #guides (colour = FALSE) + 
  ylim(c(0, 22)) + 
  labs(x = 'Frekvence [Hz]',
       y = 'Log-periodogram',
       colour = 'Foném')

(p1 | p2 | p3)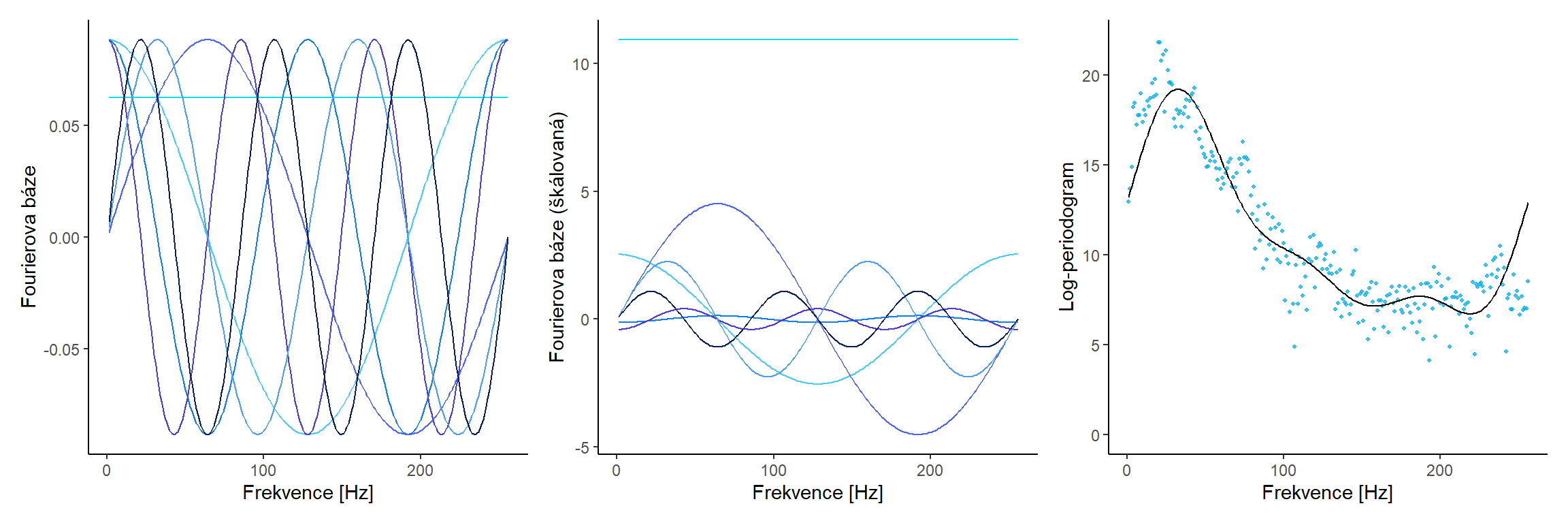

Obrázek 6.1: Fourierova baze.

Code

# dev.off()
#ggsave('figures/DP_kap1_Fbasis_nbasis7.pdf')

14.2 Materiály pro Kapitolu 2

Ve druhé sekci se podíváme na materiály pro Kapitolu 2 diplomové práce.

Bude nás zajímat vliv vyhlazovacího parametru \(\lambda\) na výslednou odhadnutou křivku z diskrétních dat. Dále se podíváme na funkcionální analýzu hlavních komponent. Nejprve se ale podívejme na vliv počtu bázových funkcí na výsledný odhad funkce.

14.2.1 Počet bázových funkcí a výsledný odhad

Code

df <- data.frame(x = 1:256, y = data[5, 2:257] |> c() |> unlist())
norder <- 4
rangeval <- range(df$x)

bbasis1 <- create.bspline.basis (rangeval, norder = norder, nbasis = 5)
BSmooth1 <- smooth.basis(df$x, df$y, bbasis1)
fdBSmootheval1 <- eval.fd(fdobj = BSmooth1$fd, evalarg = df$x)

bbasis2 <- create.bspline.basis (rangeval, norder = norder, nbasis = 15)
BSmooth2 <- smooth.basis(df$x, df$y, bbasis2)
fdBSmootheval2 <- eval.fd(fdobj = BSmooth2$fd, evalarg = df$x)

bbasis3 <- create.bspline.basis (rangeval, norder = norder, nbasis = 25)
BSmooth3 <- smooth.basis(df$x, df$y, bbasis3)
fdBSmootheval3 <- eval.fd(fdobj = BSmooth3$fd, evalarg = df$x)

# 10 bazovych funkci
p1 <- ggplot(data = df, aes(x, y)) + 
  # geom_vline(xintercept = breaks, linetype = "dotted", linewidth = 0.1, colour = 'grey') +
  geom_point(colour = 'deepskyblue2', size = 0.8, alpha = 0.75) +
  geom_line(aes(y = fdBSmootheval1), linewidth = 0.7) +
  theme_classic() + 
  ylim(c(0, 22)) + 
  labs(x = 'Frekvence',
       y = 'Log-periodogram',
       colour = 'Foném')

# 10 bazovych funkci
p2 <- ggplot(data = df, aes(x, y)) + 
  # geom_vline(xintercept = breaks, linetype = "dotted", linewidth = 0.1, colour = 'grey') +
  geom_point(colour = 'deepskyblue2', size = 0.8, alpha = 0.75) +
  geom_line(aes(y = fdBSmootheval2), linewidth = 0.7) +
  theme_classic() + 
  ylim(c(0, 22)) + 
  labs(x = 'Frekvence',
       y = 'Log-periodogram',
       colour = 'Foném')

# 10 bazovych funkci
p3 <- ggplot(data = df, aes(x, y)) + 
  # geom_vline(xintercept = breaks, linetype = "dotted", linewidth = 0.1, colour = 'grey') +
  geom_point(colour = 'deepskyblue2', size = 0.8, alpha = 0.75) +
  geom_line(aes(y = fdBSmootheval3), linewidth = 0.7) +
  theme_classic() + 
  ylim(c(0, 22)) + 
  labs(x = 'Frekvence',
       y = 'Log-periodogram',
       colour = 'Foném')

# tikz(file = "figures/DP_kap2_differentnbasis.tex", width = 12, height = 4)

(p1 | p2 | p3)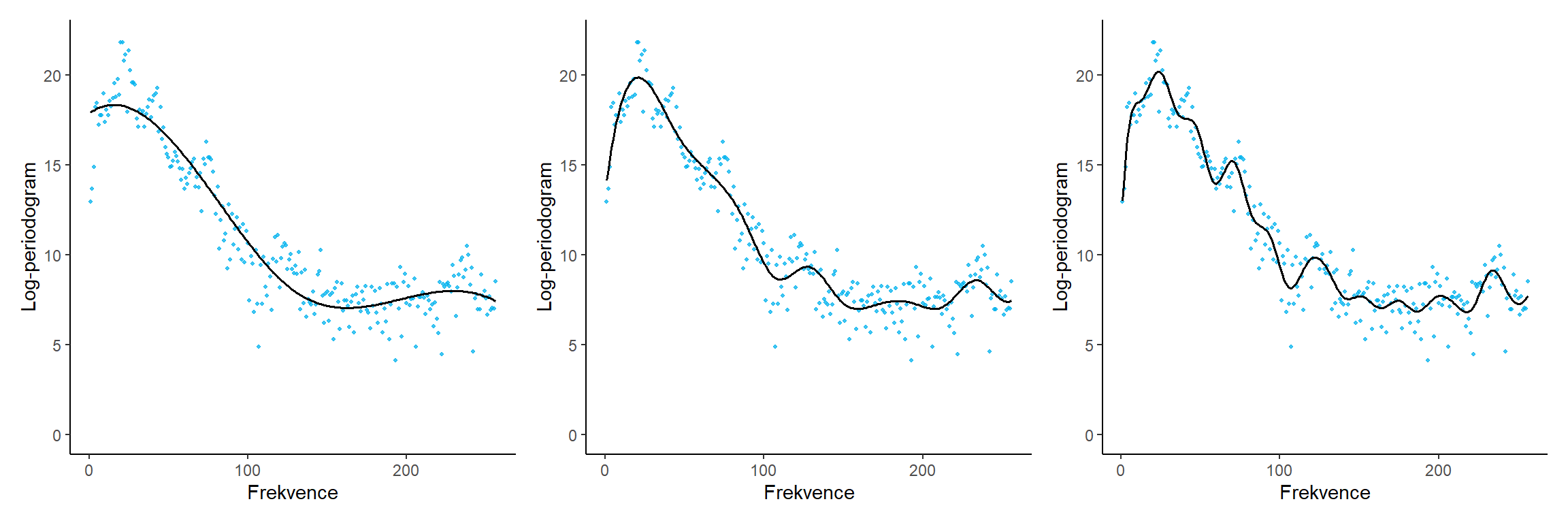

Obrázek 5.2: Počet bázových funkcí a výsledný odhad.

Code

# dev.off()
ggsave('figures/DP_kap2_differentnbasis.tex', width = 9, height = 3, device = tikz)

14.2.2 Volba \(\lambda\)

Začněme volbou vyhlazovacího parametru \(\lambda > 0\). S rostoucí hodnotou \(\lambda\) dáváme v penalizované sumě čtverců \[ SS_{pen} = (\boldsymbol y - \boldsymbol B \boldsymbol c)^\top (\boldsymbol y - \boldsymbol B \boldsymbol c) + \lambda \boldsymbol c^\top \boldsymbol R \boldsymbol c \] větší váhu penalizačnímu členu, tedy dostaneme více penalizované, více hladké křivky blížící se lineární funkci. Vykreslíme si obrázky, ve kterých bude zřejmé, jak se s měnící se hodnotou \(\lambda\) mění výsledná vyhlazená křivka.

Ke znázornění tohoto chování použijeme data phoneme z jedné z předchozích kapitol. Vybereme jedno zajímavé pozorování a ukážeme na něm toto chování.

Za uzly bereme celý vektor frekvencí (1 až 256 Hz), standardně uvažujeme kubické spliny, proto volíme (implicitní volba v R) norder = 4. Budeme penalizovat druhou derivaci funkcí.

Code

t <- 1:256
rangeval <- range(t)
breaks <- t
norder <- 4

bbasis <- create.bspline.basis(rangeval = rangeval, 
                               norder = norder, 
                               breaks = breaks)

curv.Lfd <- int2Lfd(2) # penalizujeme 2. derivaci

# spojeni pozorovani do jedne matice
XX <- cbind(X_train, X_test) |> as.matrix()

Zvolme nyní nějakých 6 hodnot pro vyhlazovací parametr \(\lambda\) a spočítejme vyhlazené křivky pro jeden vybraný záznam.

Code

lambdas <- c(0.01, 0.1, 50, 500, 10000, 1000000) # vektor lambd

tt <- seq(min(t), max(t), length = 1001)

# objekt, do ktereho ulozime hodnoty
res_plot <- matrix(NA, ncol = length(lambdas), nrow = length(tt))

for(i in 1:length(lambdas)) {
  curv.fdPar <- fdPar(bbasis, curv.Lfd, lambdas[i])
  BSmooth <- smooth.basis(t, XX, curv.fdPar)
  XXfd <- BSmooth$fd
  
  fdobjSmootheval <- eval.fd(fdobj = XXfd, evalarg = tt)[, 1]
  res_plot[, i] <- fdobjSmootheval
}

Code

options(scipen = 999)
library(scales)

lam_labs <- paste0('$\\lambda = ', lambdas, "$")
names(lam_labs) <- lambdas

# tikz(file = "figures/DP_kap2_lambdas.tex", width = 9, height = 6)

data.frame(time = rep(tt, length(lambdas)),
           value = c(res_plot),
           lambda = rep(lambdas, each = length(tt))) |>
  # mutate(lambda = factor(lambda)) |>
  ggplot(aes(x = time, y = value)) + 
  geom_point(data = data.frame(time = rep(t, length(lambdas)),
                               value = rep(c(data[5, 2:257]) |> unlist(), length(lambdas)),
                               lambda = rep(lambdas, each = length(t))) ,
             alpha = 0.5, size = 0.75, colour = "deepskyblue2") + 
  geom_line(linewidth = 0.7, colour = "grey2") + 
  facet_wrap(~lambda, ncol = 3, nrow = 2, labeller = labeller(lambda = lam_labs)) +
  theme_bw() + 
  theme(legend.position = 'none') + 
  labs(x = 'Frekvence',
       y = 'Log-periodogram',
       colour = 'Foném')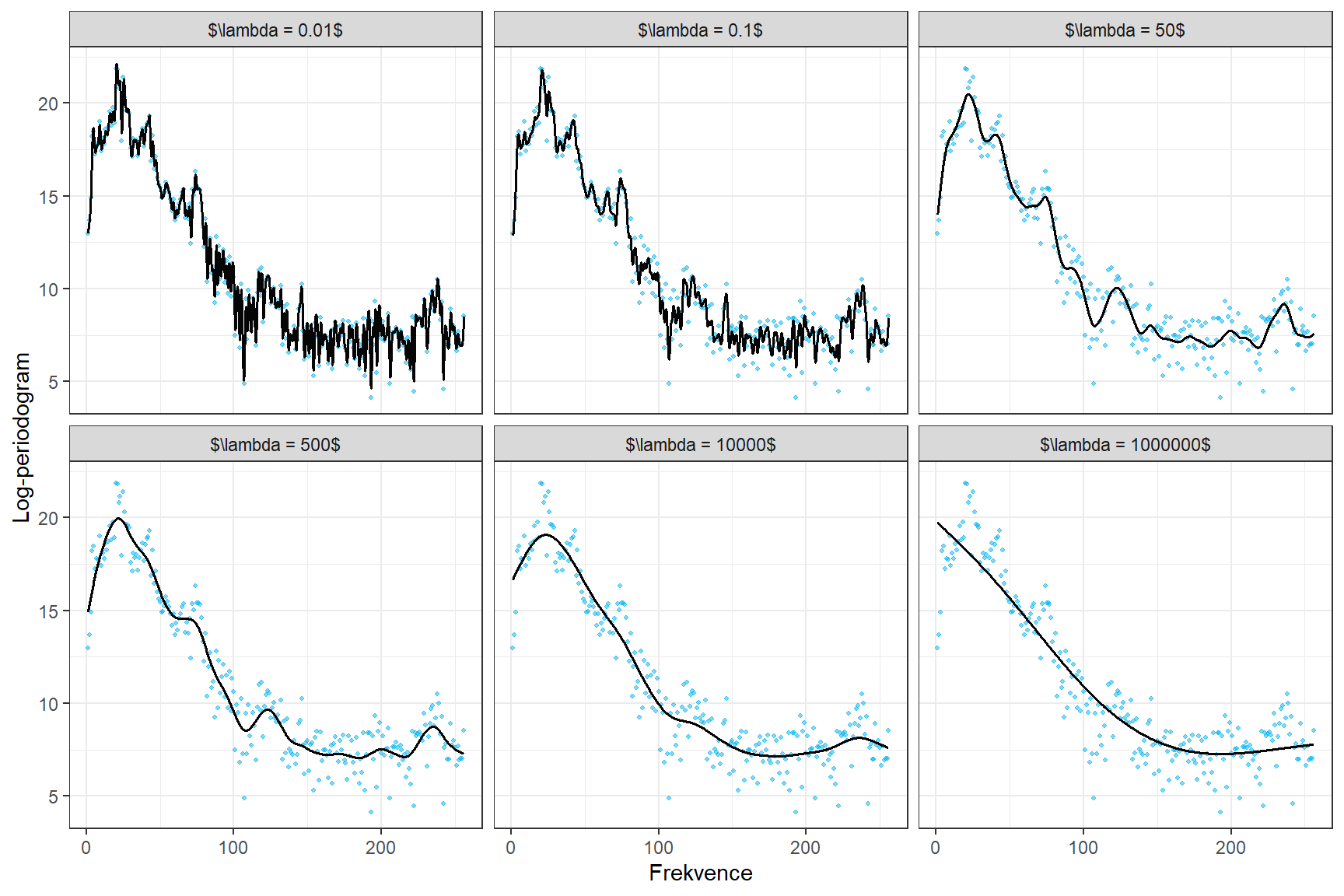

Obrázek 5.4: Log-periodogram vybraného fonému pro zvolené hodnoty vyhlazovacího parametru.

Code

  # scale_color_brewer()
# dev.off()
# ggsave('figures/DP_kap2_lambdas.pdf')

14.2.3 Vyhlazení s optimální \(\lambda\)

V Kapitole Aplikace na reálných datech 2 jsme zjistili optimální hodnotu vyhlazovacího parametru. Tu nyní použijeme.

Code

lambdas <- c(175.75)

tt <- seq(min(t), max(t), length = 1001)

# objekt, do ktereho ulozime hodnoty
res_plot <- matrix(NA, ncol = length(lambdas), nrow = length(tt))

for(i in 1:length(lambdas)) {
  curv.fdPar <- fdPar(bbasis, curv.Lfd, lambdas[i])
  BSmooth <- smooth.basis(t, XX, curv.fdPar)
  XXfd <- BSmooth$fd
  
  fdobjSmootheval <- eval.fd(fdobj = XXfd, evalarg = tt)[, 1]
  res_plot[, i] <- fdobjSmootheval
}

Code

options(scipen = 999)
library(scales)

lam_labs <- paste0('$\\lambda = ', lambdas, "$")
names(lam_labs) <- lambdas

# tikz(file = "figures/DP_kap2_optimal_lambda.tex", width = 6, height = 4)

data.frame(time = rep(tt, length(lambdas)),
           value = c(res_plot),
           lambda = rep(lambdas, each = length(tt))) |>
  # mutate(lambda = factor(lambda)) |>
  ggplot(aes(x = time, y = value)) + 
  geom_point(data = data.frame(time = rep(t, length(lambdas)),
                               value = rep(c(data[5, 2:257]) |> unlist(), length(lambdas)),
                               lambda = rep(lambdas, each = length(t))) ,
             alpha = 0.5, size = 0.75, colour = "deepskyblue2") + 
  geom_line(linewidth = 0.7, colour = "grey2") + 
  # facet_wrap(~lambda, ncol = 3, nrow = 2, labeller = labeller(lambda = lam_labs)) +
  theme_bw() + 
  theme(legend.position = 'none') + 
  labs(x = 'Frekvence',
       y = 'Log-periodogram',
       colour = 'Foném')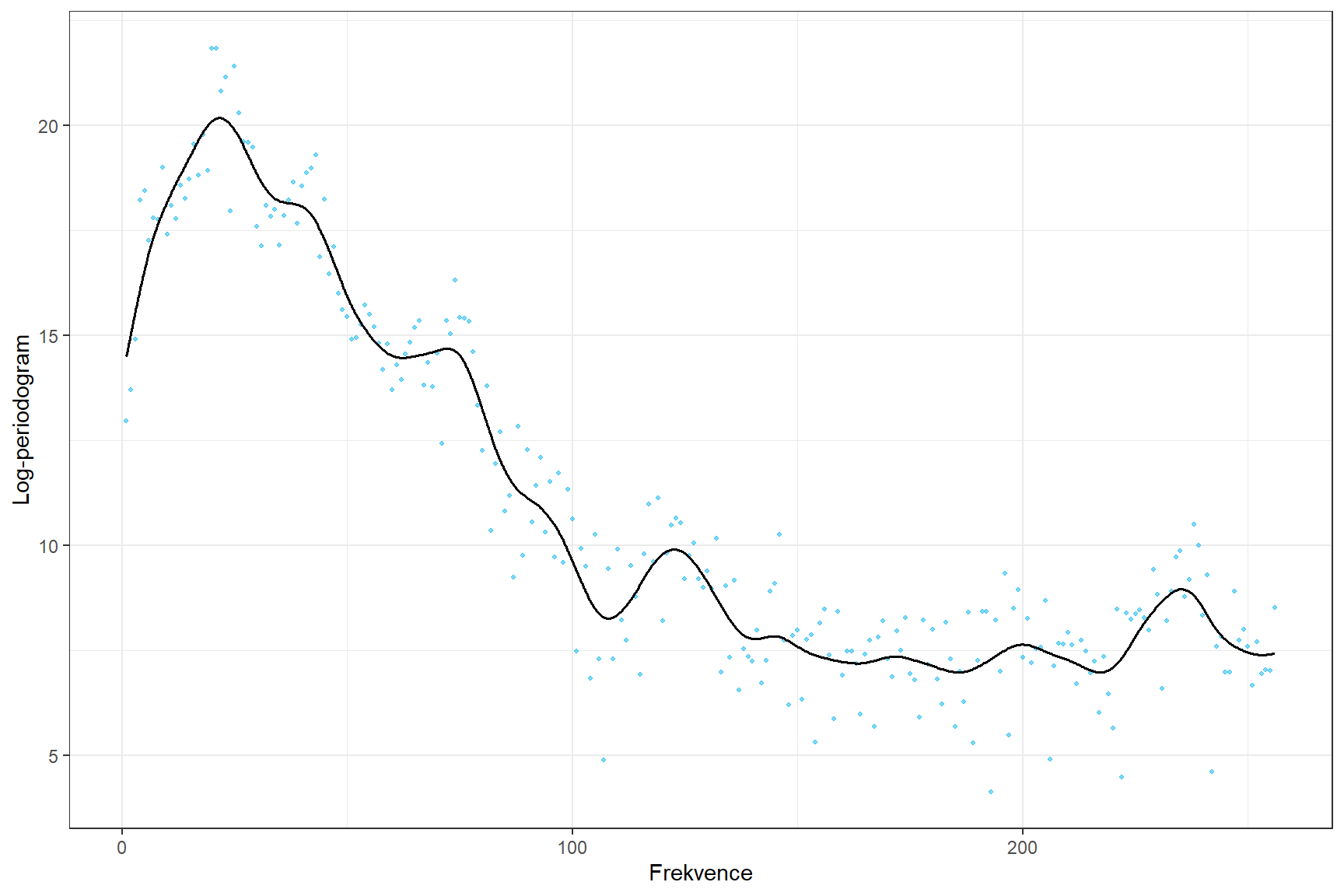

Obrázek 2.4: Log-periodogram vybraného fonému pro zvolené hodnoty vyhlazovacího parametru.

Code

  # scale_color_brewer()
# dev.off()
# ggsave('figures/DP_kap2_lambdas.pdf')

14.2.4 Funkcionální PCA

Najdeme vhodnou hodnotu vyhlazovacího parametru \(\lambda > 0\) pomocí \(GCV(\lambda)\), tedy pomocí zobecněné cross–validace.

Code

t <- 1:256
rangeval <- range(t)
breaks <- t
norder <- 4

bbasis <- create.bspline.basis(rangeval = rangeval, 
                               norder = norder, 
                               breaks = breaks)

curv.Lfd <- int2Lfd(2) # penalizujeme 2. derivaci

Code

# spojeni pozorovani do jedne matice
XX <- cbind(X_train, X_test) |> as.matrix()

lambda.vect <- 10^seq(from = 1, to = 3, length.out = 35) # vektor lambd
gcv <- rep(NA, length = length(lambda.vect)) # prazdny vektor pro ulozebi GCV

for(index in 1:length(lambda.vect)) {
  curv.Fdpar <- fdPar(bbasis, curv.Lfd, lambda.vect[index])
  BSmooth <- smooth.basis(t, XX, curv.Fdpar) # vyhlazeni
  gcv[index] <- mean(BSmooth$gcv) # prumer pres vsechny pozorovane krivky
}

GCV <- data.frame(
  lambda = round(log10(lambda.vect), 3),
  GCV = gcv
)

# najdeme hodnotu minima
lambda.opt <- lambda.vect[which.min(gcv)]

S touto optimální volbou vyhlazovacího parametru \(\lambda\) nyní vyhladíme všechny funkce.

Code

curv.fdPar <- fdPar(bbasis, curv.Lfd, lambda.opt)
BSmooth <- smooth.basis(t, XX, curv.fdPar)
XXfd <- BSmooth$fd

fdobjSmootheval <- eval.fd(fdobj = XXfd, evalarg = t)

Proveďme tedy nejprve funkcionální analýzu hlavních komponent a určeme počet \(p\).

Code

# analyza hlavnich komponent
data.PCA <- pca.fd(XXfd, nharm = 20) # nharm - maximalni pocet HK
nharm <- which(cumsum(data.PCA$varprop) >= 0.9)[1] # urceni p

# data.PCA <- pca.fd(XXfd, nharm = 20) 
data.PCA.train <- as.data.frame(data.PCA$scores) # skore prvnich p HK
data.PCA.train$Y <- factor(y) # prislusnost do trid

V tomto konkrétním případě jsme za počet hlavních komponent vzali \(p\) = 9, které dohromady vysvětlují 90.47 % variability v datech. První hlavní komponenta potom vysvětluje 44.79 % a druhá 13.37 % variability. Graficky si můžeme zobrazit hodnoty skórů prvních dvou hlavních komponent, barevně odlišených podle příslušnosti do klasifikační třídy.

Code

p1 <- data.PCA.train |> ggplot(aes(x = V1, y = V2, colour = Y)) +
  geom_point(size = 1.2, alpha = 0.75) + 
  labs(x = paste('1. hlavní komponenta (', 
                 round(100 * data.PCA$varprop[1], 2), '\\%)'),
       y = paste('2. hlavní komponenta (', 
                 round(100 * data.PCA$varprop[2], 2), '\\%)'),
       colour = 'Foném') +
  # scale_colour_discrete(labels = phoneme_subset) +
  theme_bw() + 
  theme(legend.position = 'none') + 
  lims(x = c(-70, 62), y = c(-70, 62)) +
  scale_colour_manual(values = c('tomato', 'deepskyblue2'))

p2 <- data.PCA.train |> ggplot(aes(x = V1, y = V3, colour = Y)) +
  geom_point(size = 1.2, alpha = 0.75) + 
  labs(x = paste('1. hlavní komponenta (', 
                 round(100 * data.PCA$varprop[1], 2), '\\%)'),
       y = paste('3. hlavní komponenta (', 
                 round(100 * data.PCA$varprop[3], 2), '\\%)'),
       colour = 'Foném') +
  # scale_colour_discrete(labels = phoneme_subset) +
  theme_bw() + 
  theme(legend.position = 'none') + 
  lims(x = c(-70, 62), y = c(-70, 62)) +
  scale_colour_manual(values = c('tomato', 'deepskyblue2'))

p3 <- data.PCA.train |> ggplot(aes(x = V2, y = V3, colour = Y)) +
  geom_point(size = 1.2, alpha = 0.75) + 
  labs(x = paste('2. hlavní komponenta (', 
                 round(100 * data.PCA$varprop[2], 2), '\\%)'),
       y = paste('3. hlavní komponenta (', 
                 round(100 * data.PCA$varprop[3], 2), '\\%)'),
       colour = 'Foném') +
  # scale_colour_discrete(labels = phoneme_subset) +
  theme_bw() + 
  lims(x = c(-70, 62), y = c(-70, 62)) +
  theme(legend.position = c(0.84, 0.84)) +
  scale_colour_manual(values = c('tomato', 'deepskyblue2'))

(p1|p2|p3)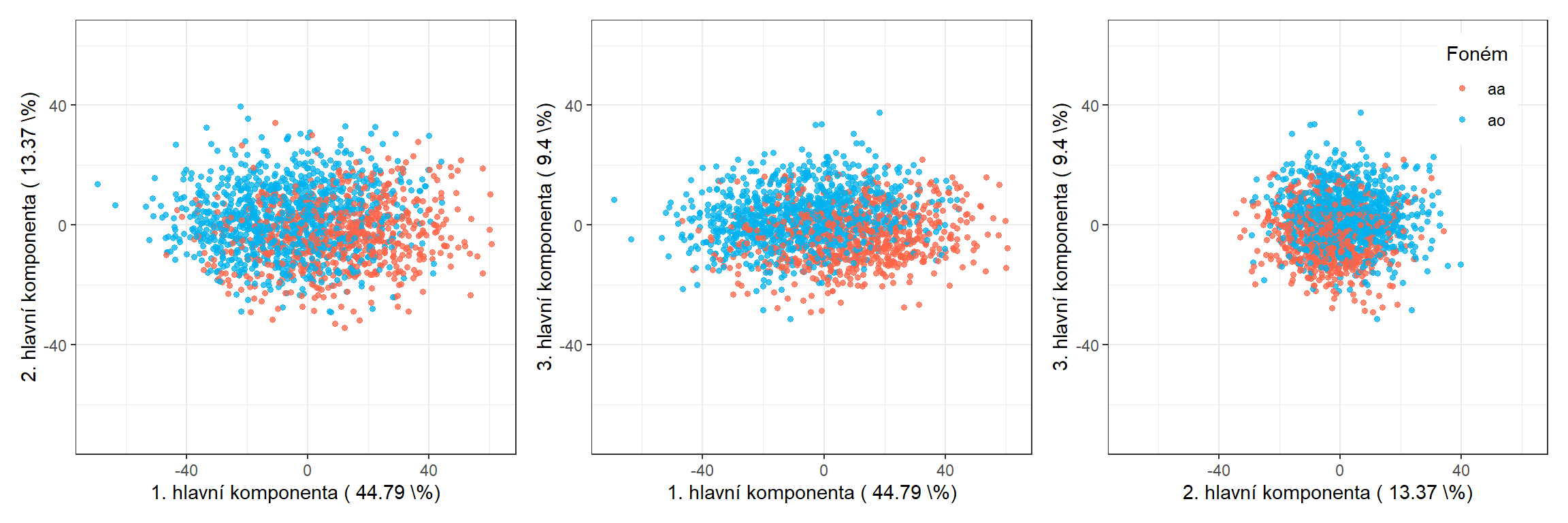

Hodnoty skórů prvních tří hlavních komponent pro trénovací data. Barevně jsou odlišeny body podle příslušnosti do klasifikační třídy.

Obrázek 5.5: Hodnoty skórů prvních tří hlavních komponent pro trénovací data. Barevně jsou odlišeny body podle příslušnosti do klasifikační třídy.

Code

# tikz(file = "figures/kap2_PCA_scores1.tex", width = 3, height = 3)
# p1
# dev.off()
# tikz(file = "figures/kap2_PCA_scores2.tex", width = 3, height = 3)
# p2
# dev.off()
# tikz(file = "figures/kap2_PCA_scores3.tex", width = 3, height = 3)
# p3
# dev.off()
# ggsave("figures/kap2_PCA_scores.tex", device = tikz, width = 12, height = 4)

Podívejme se ještě na 3D graf skórů prvních třech hlavních komponent.

Code

# 3D plot 
library(plotly)
plot_ly(data = data.PCA.train,
        x = ~V1, y = ~V2, z = ~V3,
        color = ~Y, colors = c('tomato', 'deepskyblue2'),
        type="scatter3d", mode="markers", marker = list(size = 2.5)) %>% 
  layout(scene = list(xaxis = list(title = '1. hlavní komponenta'),
                     yaxis = list(title = '2. hlavní komponenta'),
                     zaxis = list(title = '3. hlavní komponenta')))

Obrázek 3.5: 3D graf skórů prvních třech hlavních komponent.

Vykresleme si i průběh kumulativní vysvětlené variability.

Code

data.frame(x = 1:15,
           y = pca.fd(XXfd, nharm = 15)$varprop |> cumsum() * 100) |>
  ggplot(aes(x, y)) + 
  geom_point(col = 'deepskyblue2') + 
  geom_line(col = 'deepskyblue2') + 
  theme_bw() + 
  labs(x = 'Počet hlavních komponent',
       y = "Kumulativní vysvětlená variabilita [v \\%]") + 
  geom_hline(aes(yintercept = 90), linetype = 'dashed', col = 'grey2') + 
  scale_x_continuous(breaks = 1:15) + 
  theme(panel.grid.minor.x = element_blank(),
        panel.grid.minor.y = element_blank())

Obrázek 2.5: Kumulativní vysvětlená variabilita [v %] proti počtu hlavních komponent.

Code

# ggsave("figures/kap2_PCA_nharm.tex", device = tikz, width = 5, height = 3)

Také nás zajímá průběh prvních třech funkcionálních hlavních komponent.

Code

## Looking at the principal components:

fdobjPCAeval <- eval.fd(fdobj = data.PCA$harmonics[1:3], evalarg = t)
df.comp <- data.frame(
  time = t, 
  harmonics = c(fdobjPCAeval), 
  component = factor(rep(1:3, each = 256))
  )

df.comp |> ggplot(aes(x = time, y = harmonics, color = component)) + 
  geom_line(linewidth = 0.7) +
  labs(x = "Frekvence", 
       y = "Hlavní komponenty",
       colour = '') +
  theme_bw() + 
  scale_color_manual(values=c("#127DE8", "#4C3CD3", "#12DEE8"))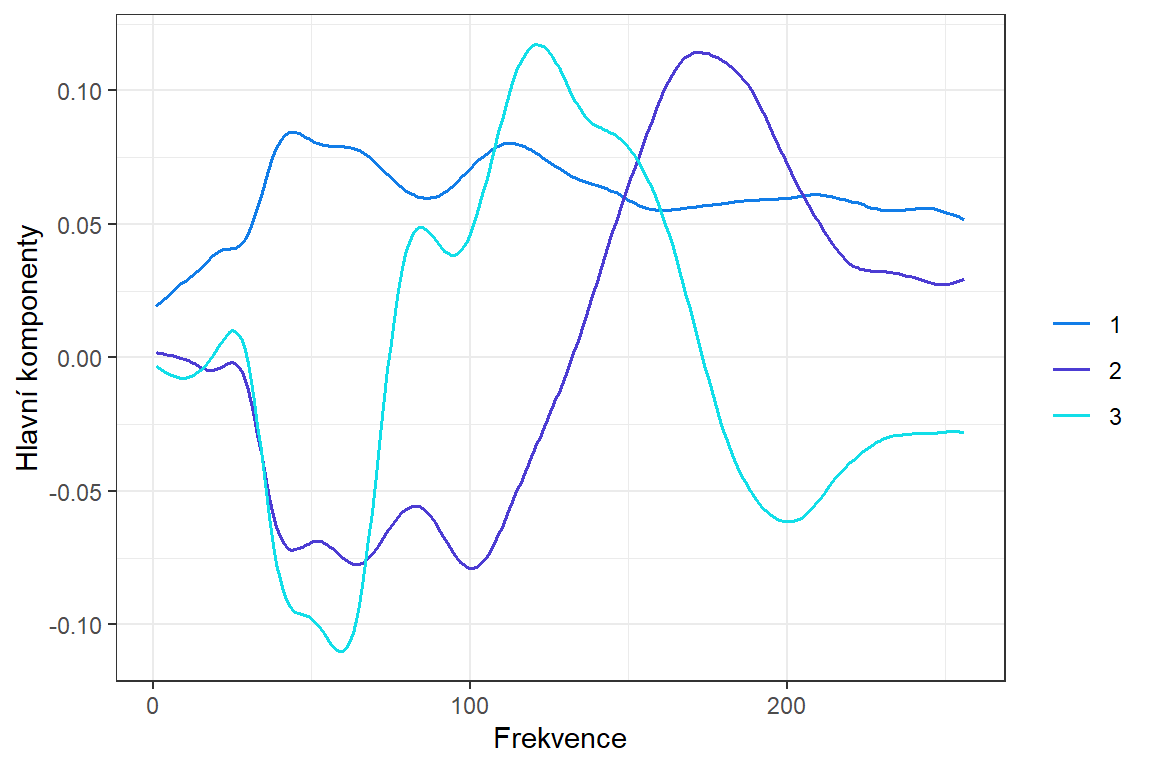

Obrázek 7.2: Hlavní komponenty.

Code

# ggsave("figures/kap2_PCA_components.tex", device = tikz, width = 5, height = 3)

Můžeme se také podívat na vliv prvních třech hlavních komponent na průměrnou křivku. Vždy je od průměru přičten nebo odečten dvojnásobek hlavní komponenty (škálovaný rozptylem).

Code

library(plyr)
freq3 <- seq(1,256)
fdobjPCAeval3 <- eval.fd(fdobj = data.PCA$harmonics[1:3], evalarg = freq3)

df.comp3 <- data.frame(
  freq = freq3, 
  harmonics = c(fdobjPCAeval3), 
  component = factor(rep(1:3, each = length(freq3)))
  )

fdm3 <- c(eval.fd(fdobj = meanfd, evalarg = freq3))

df.3 <- data.frame(df.comp3, m = fdm3)
df.pv3 <- ddply(df.3, .(component), mutate, 
                m1 = m + 2*sqrt(data.PCA$values[component])*harmonics,
                m2 = m - 2*sqrt(data.PCA$values[component])*harmonics,
                pov = paste0("Komponenta ", 
                             component,", Vysvětlená variabilita = ",
                             round(100*data.PCA$varprop[component], 1), 
                             ' \\%'))

df.pv3 |> ggplot(aes (x = freq, y = m)) +
  geom_line() +
  geom_line(aes(y = m1), linetype = 'solid', color = 'deepskyblue2') +
  geom_line(aes(y = m2), linetype = 'dashed', color = 'deepskyblue2') +
  labs(x = "Frekvence", 
       y = "Log-periodogram",
       colour = 'Komponenta') +
  theme_bw() +
  theme(legend.position = 'none') + 
  facet_wrap(~ pov, nrow = 1)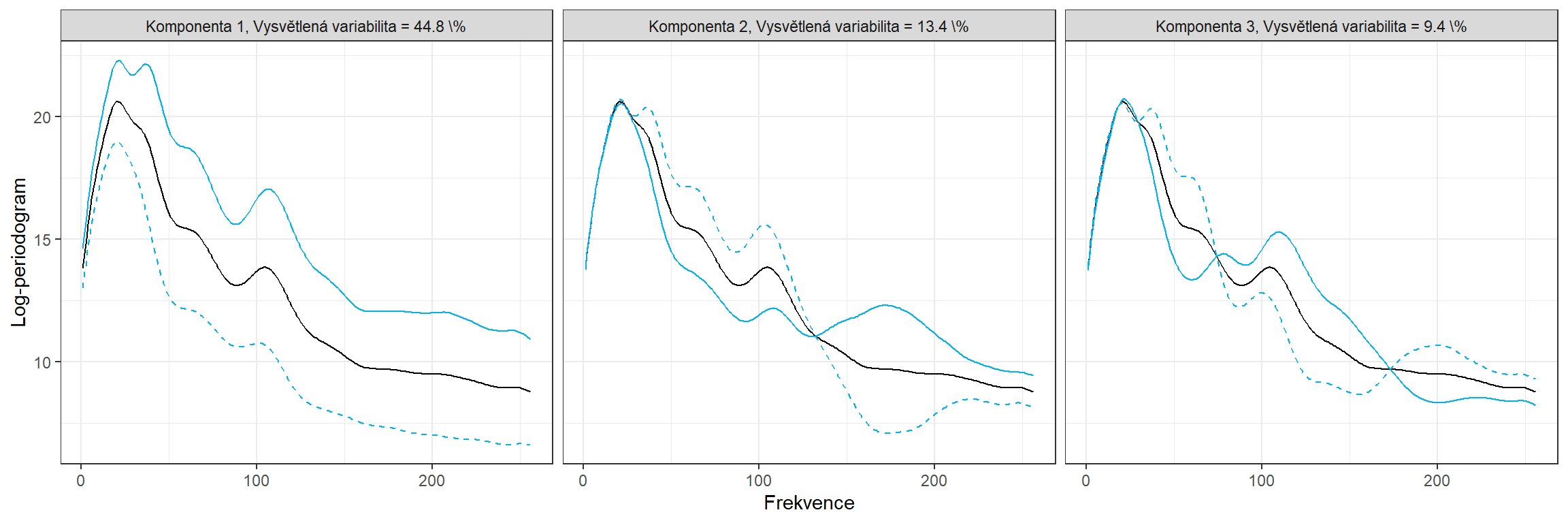

Obrázek 5.6: Vliv komponent.

Code

# ggsave("figures/kap2_PCA_impactofcomponents.tex", device = tikz, width = 9, height = 3)

Podívejme se ještě na rekonstrukci původního log-periodogramu pomocí hlavních komponent. Nejprve uvažujme pouze průměr.

Code

meanfd <- mean.fd(XXfd)
fdm <- eval.fd(fdobj = meanfd, evalarg = t)
colnames(fdm) <- NULL
scores <- data.PCA$scores
PCs <- eval.fd(fdobj = data.PCA$harmonics, evalarg = t) # vyhodnoceni

df <- data.frame(dfs[1:256, ], reconstruction =  fdm, estimate = "mean")
p0 <- ggplot(data = df, aes (x = time, y = value)) +
  geom_line(color = "grey2", linewidth = 0.5, alpha = 0.7) +
  geom_line(aes(y = reconstruction), colour = "deepskyblue2", linewidth = 0.6) +
  labs(x = "Frekvence", y = "Log-periodogram") +
  theme_bw()
print(p0)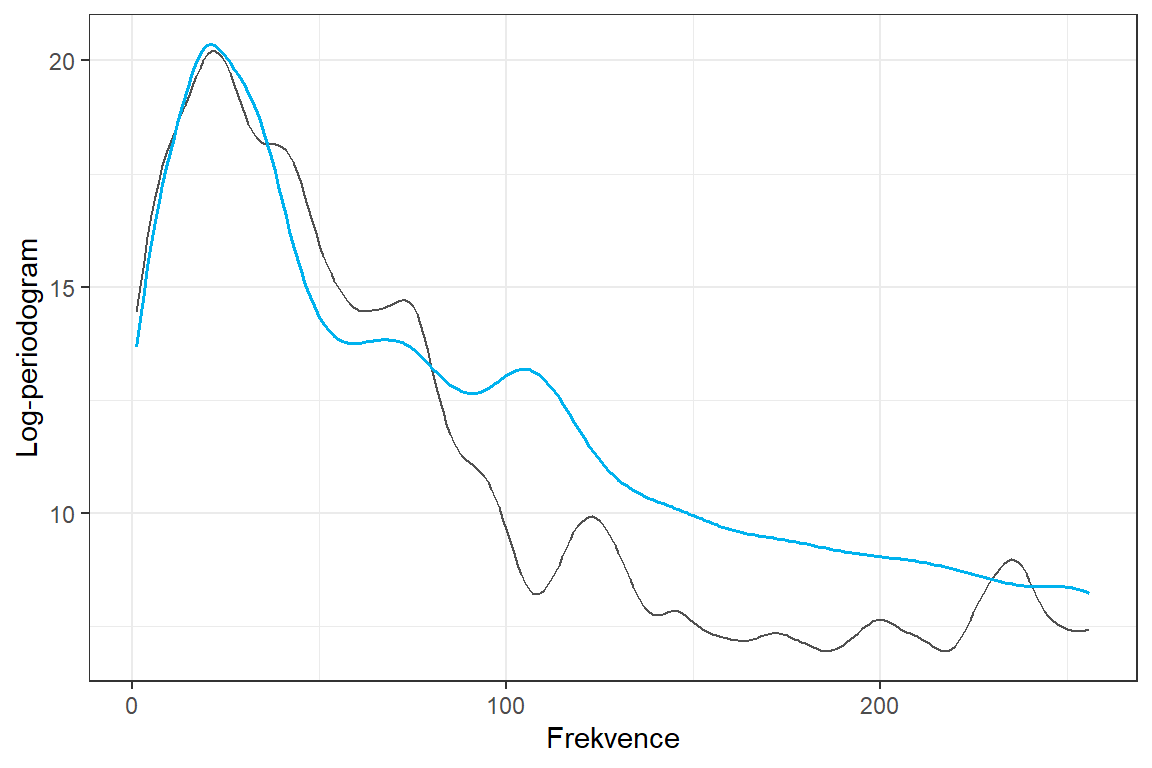

Obrázek 1.9: Původní křivka a průměr.

Konečně se podívejme na vybraný počet hlavních komponent a příslušnou rekonstrukci.

Code

for (k in 1:20){
 df1 <- data.frame(dfs[1:256, ], 
                   reconstruction = fdm + c(PCs[, 1:k] %*% 
                                              t(scores[, 1:k]))[1:256],
                   estimate = paste0("comp", k))
 df <- rbind(df, df1)
 p1 <- ggplot(data = df1, aes (x = time, y = value)) +
  geom_line(color = "grey2", linewidth = 0.5, alpha = 0.7) +
  geom_line(aes(y = reconstruction), colour = "deepskyblue2", linewidth = 0.6) +
  labs(x = "Frekvence", y = "Log-periodogram") +
  theme_bw()
 # print(p1)
}

df |> mutate(estimate = factor(estimate)) |>
  filter(estimate %in% c('mean', 'comp1', 'comp2', 'comp3', 'comp9', 'comp20')) |> 
  mutate(estimate = factor(estimate, levels = c('mean', 'comp1', 'comp2', 'comp3', 'comp9', 'comp20'))) |> 
  ggplot(aes (x = time, y = value)) +
  geom_line(color = "grey2", linewidth = 0.5, alpha = 0.5) +
  geom_line(aes(y = reconstruction), colour = "deepskyblue2", linewidth = 0.7) +
  labs(x = "Frekvence", y = "Log-periodogram") +
  theme_bw() + 
  facet_wrap(~estimate, ncol = 3, nrow = 2)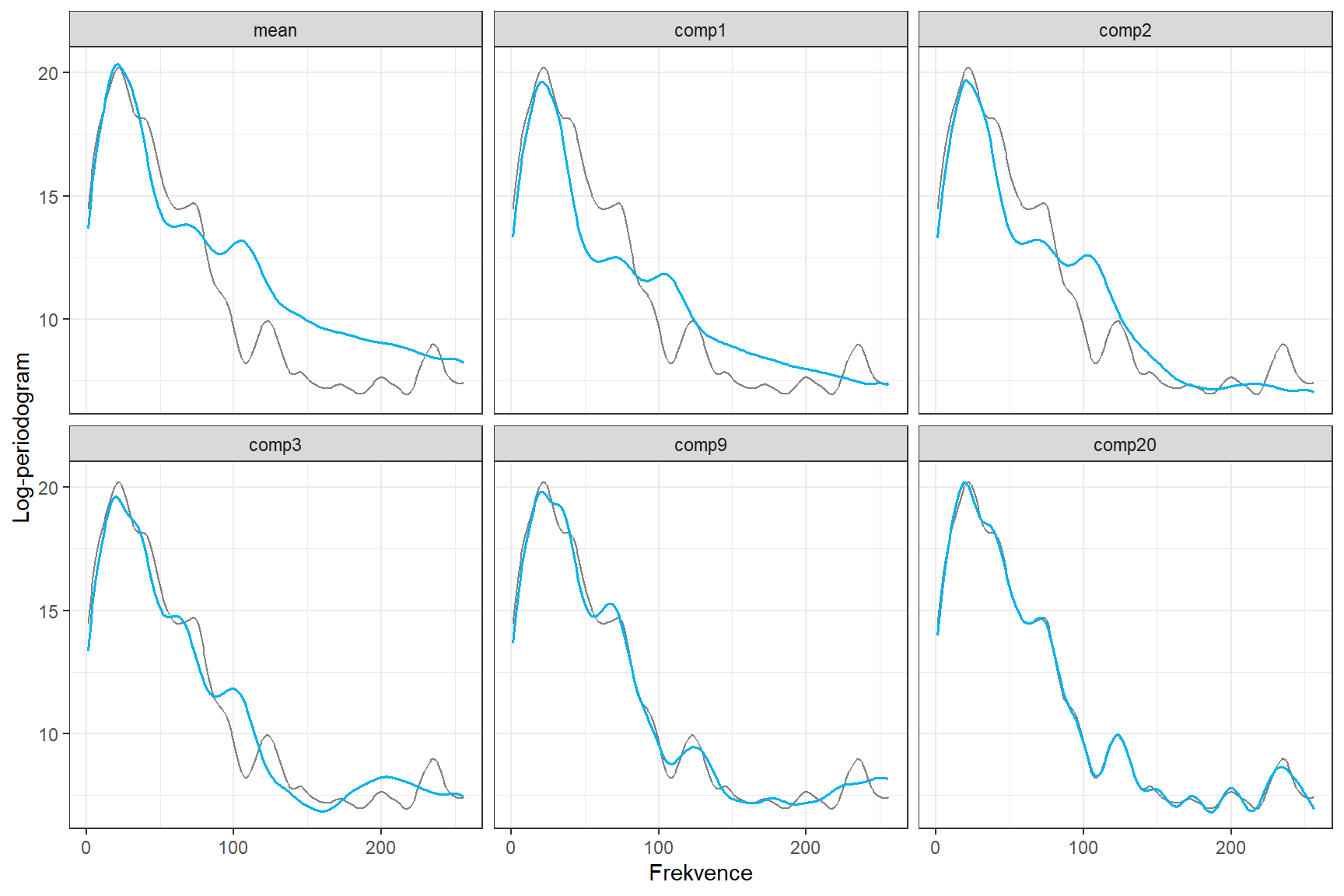

Obrázek 7.3: Původní křivka a její rekonstrukce.

Code

# ggsave("figures/kap2_PCA_reconstruction.tex", device = tikz, width = 9, height = 6)

14.3 Materiály pro Kapitolu 3

Tyto materiály jsou převzaty z Kapitoly 11.

14.4 Materiály pro Kapitolu 4

V této sekci uvedeme podpůrné grafy pro čtvrtou kapitolu diplomové práce.

14.4.1 Maximal margin classifier

Nejprve simulujeme data ze dvou klasifikačních tříd, které budou lineárně separabilní.

Code

library(MASS)
library(dplyr)
library(ggplot2)

set.seed(21)

# simulace dat
n_0 <- 40
n_1 <- 40
mu_0 <- c(0, 0)
mu_1 <- c(3, 4.5)
Sigma_0 <- matrix(c(1.3, -0.7, -0.7, 1.3), ncol = 2)
Sigma_1 <- matrix(c(1.5, -0.25, -0.25, 1.5), ncol = 2)

df_MMC <- rbind(
  mvrnorm(n = n_0, mu = mu_0, Sigma = Sigma_0),
  mvrnorm(n = n_1, mu = mu_1, Sigma = Sigma_1)) |>
  as.data.frame() |>
  mutate(Y = rep(c('-1', '1'), c(n_0, n_1)))
colnames(df_MMC) <- c('x1', 'x2', 'Y')

Nyní vykreslíme data.

Code

p1 <- ggplot(data = df_MMC,
             aes(x = x1, y = x2, colour = Y)) + 
  geom_point() + 
  theme_bw() + 
  theme(panel.grid.major = element_blank(),
        panel.grid.minor = element_blank(),
        legend.title.align = 0.5) + 
  scale_x_continuous(breaks = seq(-2, 6, by = 2), 
                     limits = c(-3.5, 6.5)) + 
  scale_y_continuous(breaks = seq(-4, 8, by = 2),
                     limits = c(-2.5, 7)) + 
  scale_colour_manual(values = c('tomato', 'deepskyblue2')) + 
  labs(x = '$X_1$', y = '$X_2$', colour = 'Klasifikační\n třída')

p1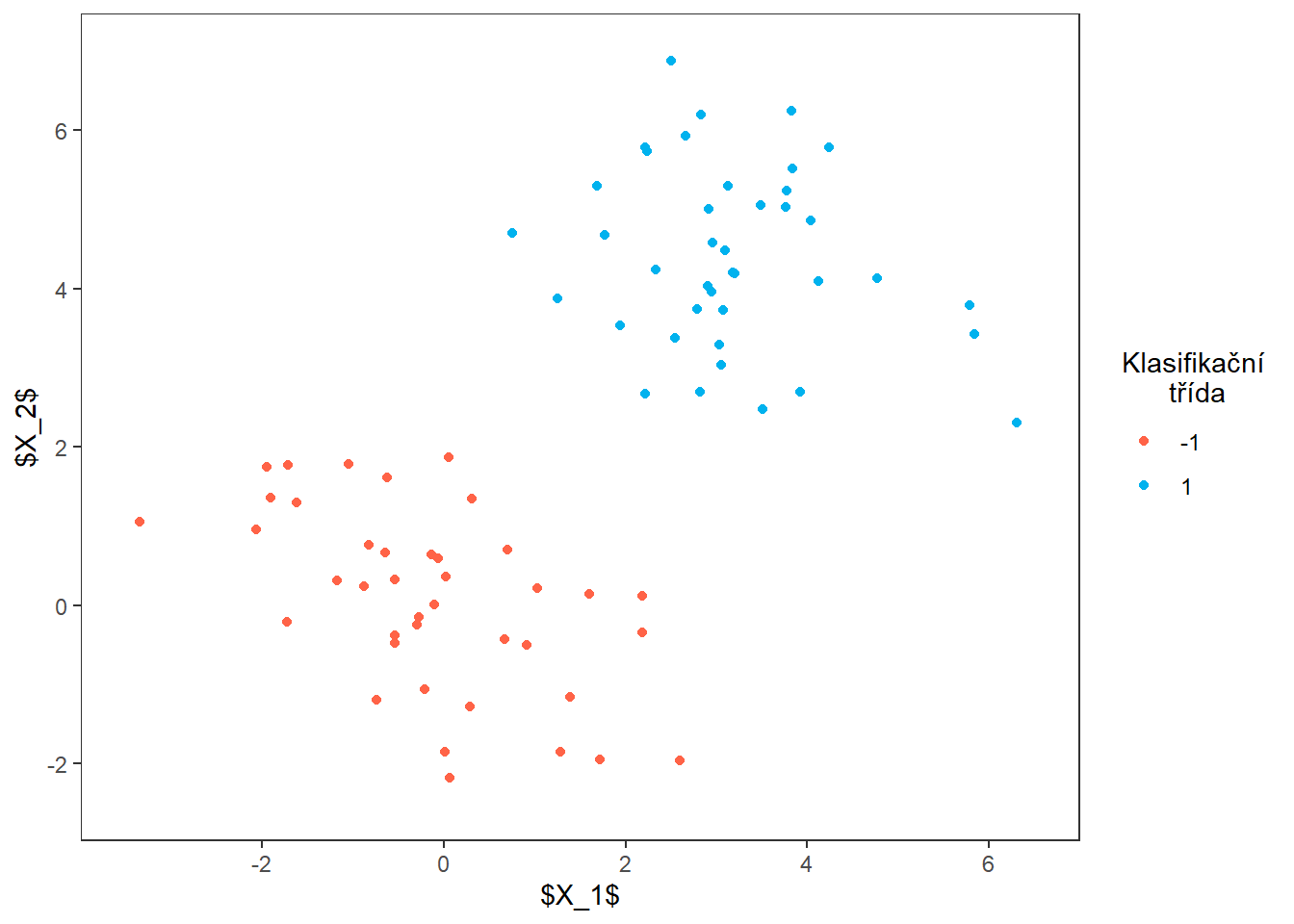

Natrénujeme klasifikátor a vykreslíme dělicí nadrovinu společně s podpůrnými vektory.

Code

library(e1071)

clf <- svm(Y ~ ., data = df_MMC,
                 type = 'C-classification',
                 scale = FALSE,
                 kernel = 'linear')

Code

df_SV <- df_MMC[clf$index, ]
p2 <- p1 + geom_point(data = df_SV, col = 'grey2', alpha = 0.7,
                      size = 2)
p2

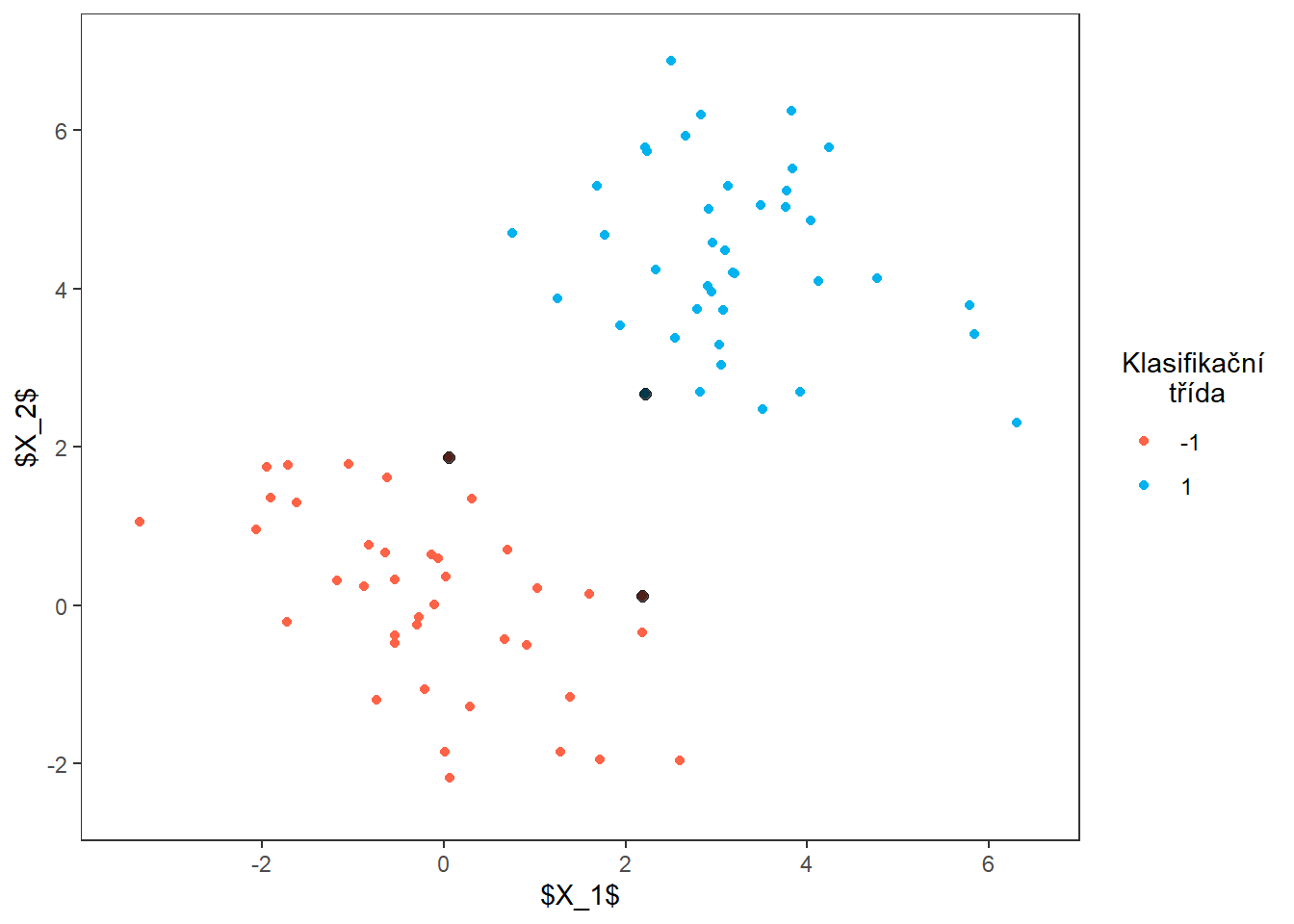
Dokreslíme dělicí nadrovinu.

Code

# vektor koeficientů
w <- t(clf$coefs) %*% clf$SV

slope <- - w[1] / w[2]
intercept <- clf$rho / w[2]

p3 <- p2 + 
  geom_abline(slope = slope, 
              intercept = intercept,
              col = 'grey2', linewidth = 0.7, alpha = 0.8) + 
  geom_abline(slope = slope, 
              intercept = intercept - 1 / w[2],
              col = 'grey2', linewidth = 0.5, alpha = 0.8,
              linetype = 'dashed') + 
  geom_abline(slope = slope, 
              intercept = intercept + 1 / w[2],
              col = 'grey2', linewidth = 0.5, alpha = 0.8,
              linetype = 'dashed') + 
  geom_point() + 
  geom_point(data = df_SV, col = 'grey2', alpha = 0.4,
                      size = 2)

p3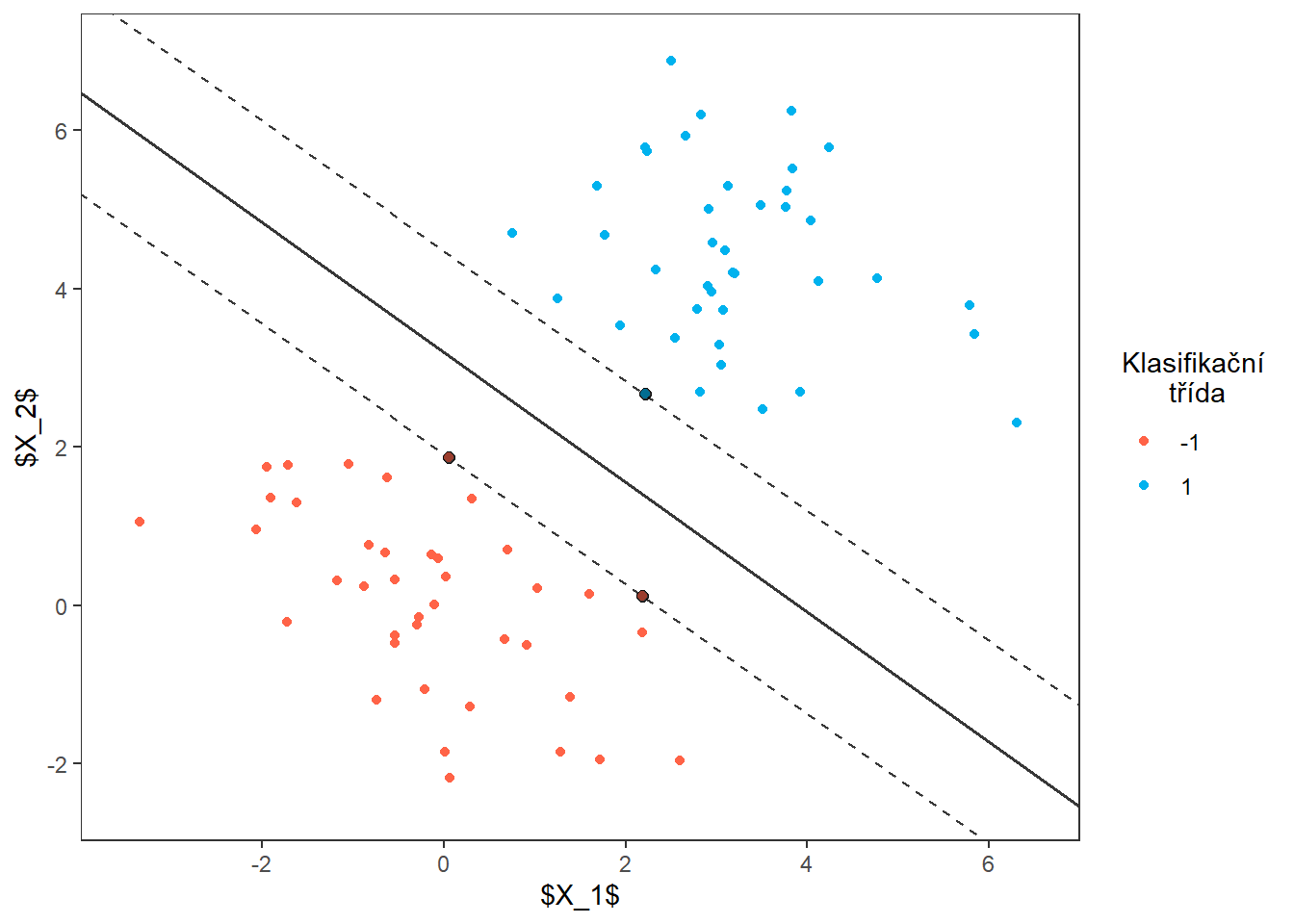

Code

# ggsave("figures/kap4_MMC.tex", device = tikz, width = 6, height = 4)

14.4.2 Support vector classifier

Nejprve simulujeme data ze dvou klasifikačních tříd, které budou lineárně neseparabilní.

Code

set.seed(42)

# simulace dat
n_0 <- 50
n_1 <- 50
mu_0 <- c(0, 0)
mu_1 <- c(3, 4.5)
Sigma_0 <- matrix(c(2, -0.55, -0.55, 2), ncol = 2)
Sigma_1 <- matrix(c(2.75, -0.3, -0.3, 2.75), ncol = 2)

df_MMC <- rbind(
  mvrnorm(n = n_0, mu = mu_0, Sigma = Sigma_0),
  mvrnorm(n = n_1, mu = mu_1, Sigma = Sigma_1)) |>
  as.data.frame() |>
  mutate(Y = rep(c('-1', '1'), c(n_0, n_1)))
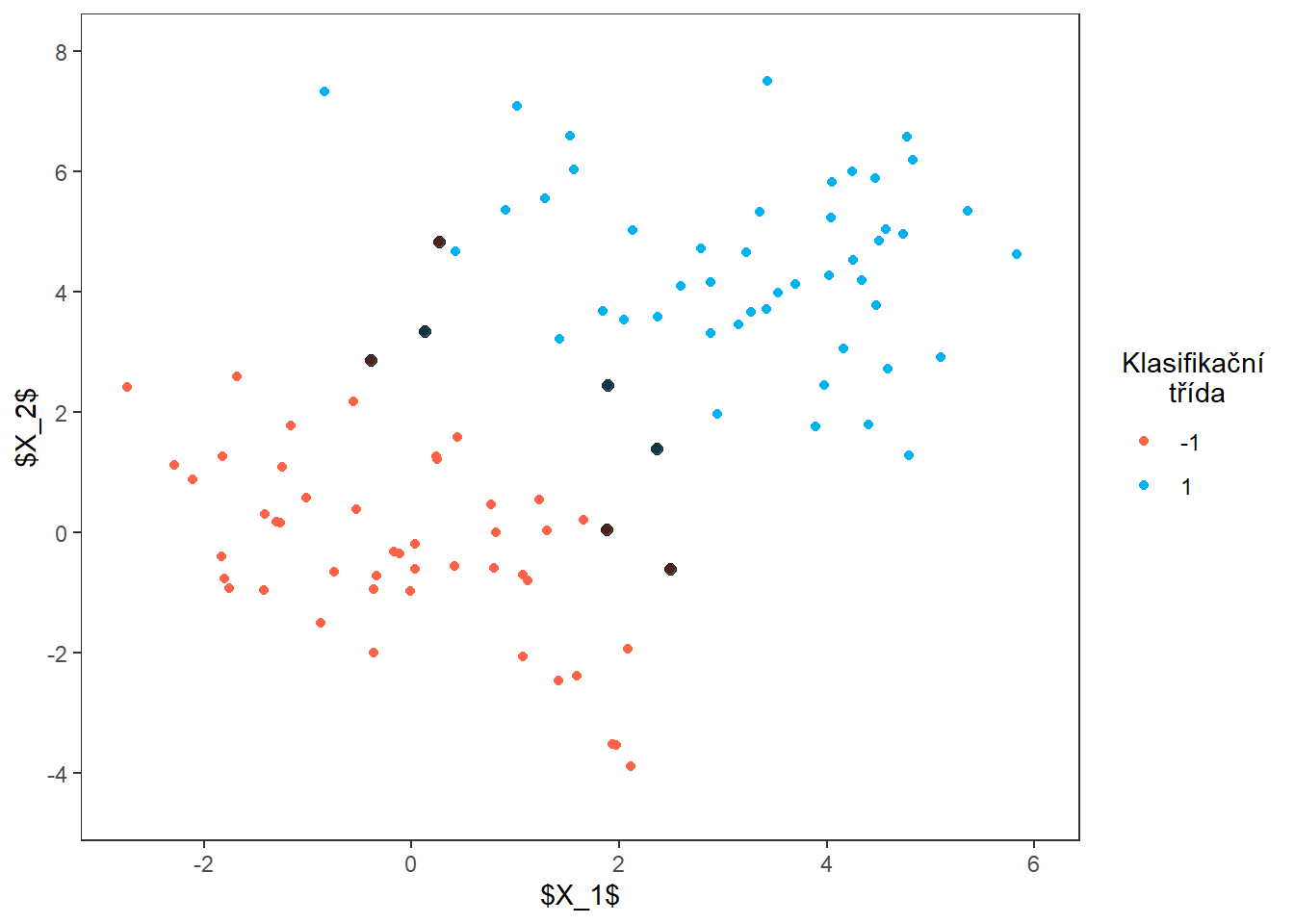
colnames(df_MMC) <- c('x1', 'x2', 'Y')

Nyní vykreslíme data.

Code

p1 <- ggplot(data = df_MMC,
             aes(x = x1, y = x2, colour = Y)) + 
  geom_point() + 
  theme_bw() + 
  theme(panel.grid.major = element_blank(),
        panel.grid.minor = element_blank(),
        legend.title.align = 0.5) + 
  scale_x_continuous(breaks = seq(-2, 6, by = 2),
                     limits = c(-2.75, 6)) +
  scale_y_continuous(breaks = seq(-4, 8, by = 2),
                     limits = c(-4.5, 8)) +
  scale_colour_manual(values = c('tomato', 'deepskyblue2')) + 
  labs(x = '$X_1$', y = '$X_2$', colour = 'Klasifikační\n třída')

p1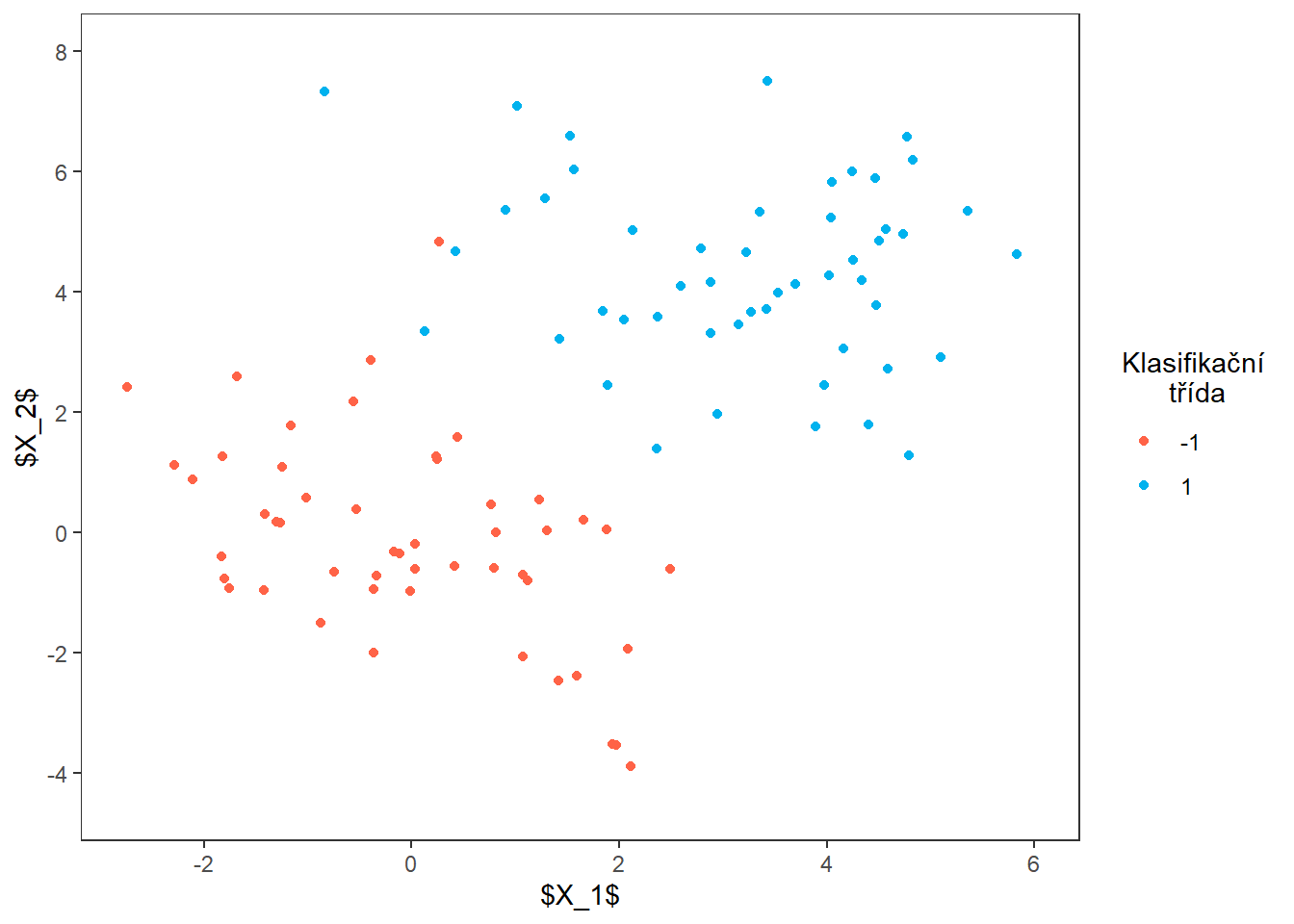

Natrénujeme klasifikátor a vykreslíme dělicí nadrovinu společně s podpůrnými vektory.

Code

clf <- svm(Y ~ ., data = df_MMC,
                 type = 'C-classification',
                 scale = FALSE,
                 kernel = 'linear')

Code

df_SV <- df_MMC[clf$index, ]
p2 <- p1 + geom_point(data = df_SV, col = 'grey2', alpha = 0.7,
                      size = 2)
p2

Dokreslíme dělicí nadrovinu.

Code

# vektor koeficientů
w <- t(clf$coefs) %*% clf$SV

slope <- - w[1] / w[2]
intercept <- clf$rho / w[2]

p3 <- p2 + 
  geom_abline(slope = slope, 
              intercept = intercept,
              col = 'grey2', linewidth = 0.7, alpha = 0.8) + 
  geom_abline(slope = slope, 
              intercept = intercept - 1 / w[2],
              col = 'grey2', linewidth = 0.5, alpha = 0.8,
              linetype = 'dashed') + 
  geom_abline(slope = slope, 
              intercept = intercept + 1 / w[2],
              col = 'grey2', linewidth = 0.5, alpha = 0.8,
              linetype = 'dashed') + 
  geom_point() + 
  geom_point(data = df_SV, col = 'grey2', alpha = 0.4,
                      size = 2)

p3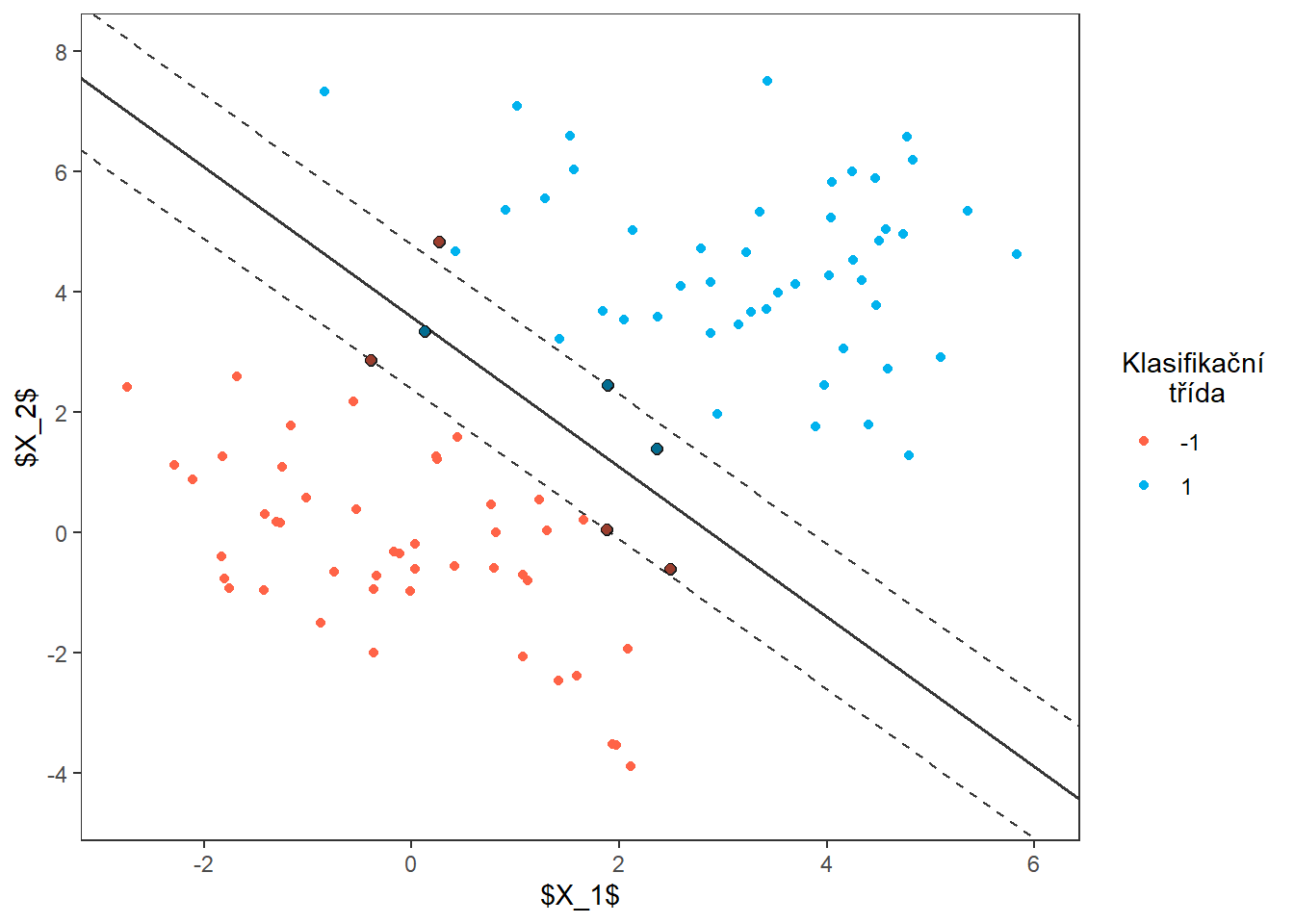

Code

# ggsave("figures/kap4_SVC.tex", device = tikz, width = 6, height = 4)

Nakonec přidáme popisky k podpůrným vektorům.

Code

df_SVlab <- cbind(df_SV, data.frame(label = 1:dim(df_SV)[1]))
p4 <- p3 + 
  geom_text(data = df_SVlab, aes(label = label), colour = 'grey2',
            check_overlap = T, size = 3, vjust = -0.55, hjust = 1)

p4

Code

# ggsave("figures/kap4_SVC.tex", device = tikz, width = 6, height = 4)

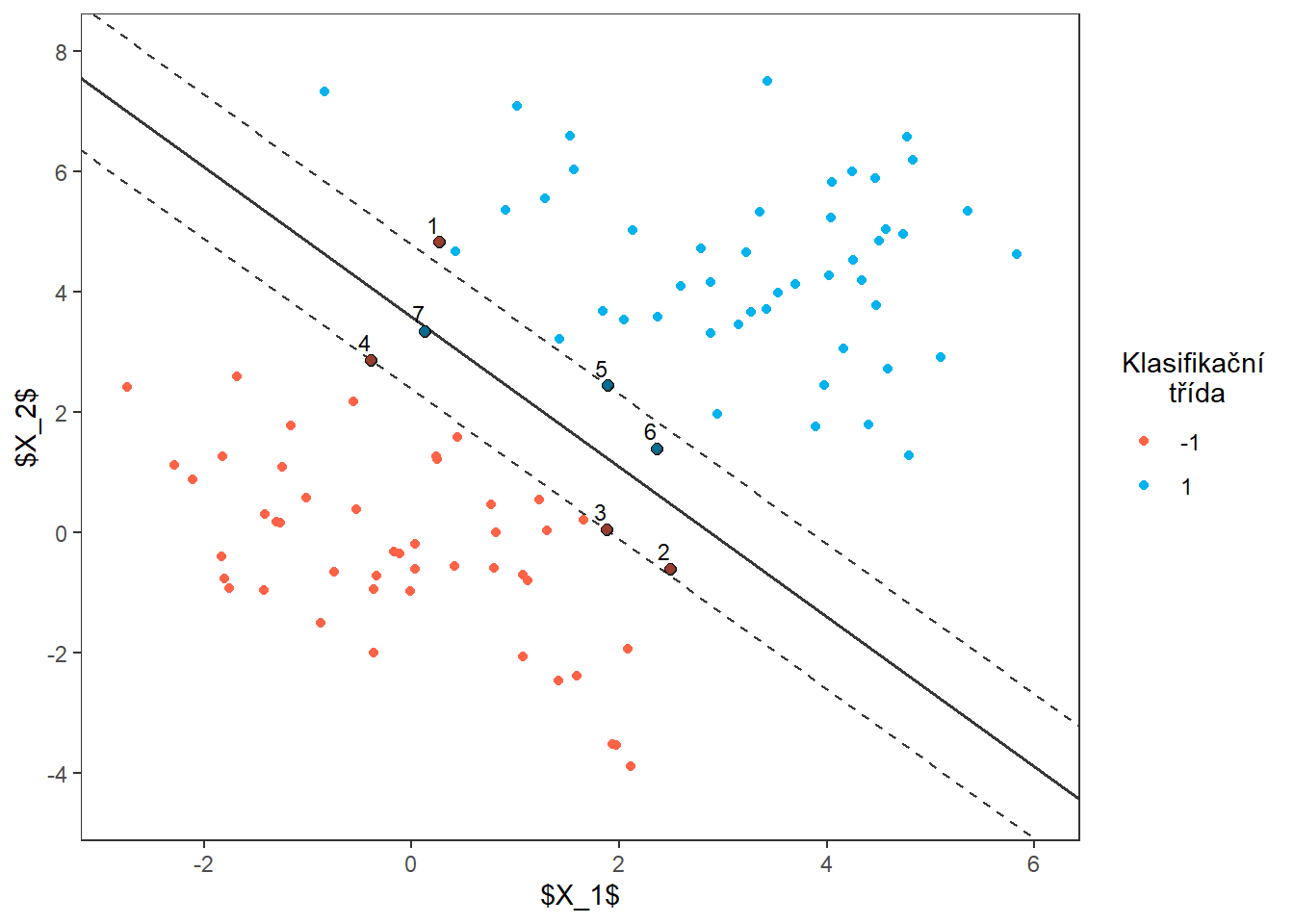
14.4.2.1 Změna šířky tolerančního pásma při změně hyperparametru \(C\)

Podívejme se ještě na změnu tolerančního pásma v závislosti na hyperparametru \(C\).

Code

C <- c(0.005, 0.1, 100)

clf1 <- svm(Y ~ ., data = df_MMC,
                 type = 'C-classification',
                 scale = FALSE,
                 kernel = 'linear',
           cost = C[1])

clf2 <- svm(Y ~ ., data = df_MMC,
                 type = 'C-classification',
                 scale = FALSE,
                 kernel = 'linear',
           cost = C[2])

clf3 <- svm(Y ~ ., data = df_MMC,
                 type = 'C-classification',
                 scale = FALSE,
                 kernel = 'linear',
           cost = C[3])

df_SV <- rbind(df_MMC[clf1$index, ] |> mutate(cost = C[1]),
               df_MMC[clf2$index, ] |> mutate(cost = C[2]),
               df_MMC[clf3$index, ] |> mutate(cost = C[3]))
p2 <- p1 + geom_point(data = df_SV, col = 'grey2', alpha = 0.7,
                      size = 2) + 
  facet_wrap(~cost)

# vektor koeficientů
w <- t(clf1$coefs) %*% clf1$SV
slope <- - w[1] / w[2]
intercept <- clf1$rho / w[2]

df_lines <- data.frame(slope = slope,
                       intercept = intercept,
                       lb = intercept - 1 / w[2],
                       rb = intercept + 1 / w[2],
                       cost = C[1])

# pro clf2
w <- t(clf2$coefs) %*% clf2$SV
slope <- - w[1] / w[2]
intercept <- clf2$rho / w[2]

df_lines <- rbind(df_lines,
                  data.frame(slope = slope,
                       intercept = intercept,
                       lb = intercept - 1 / w[2],
                       rb = intercept + 1 / w[2],
                       cost = C[2])
                  )

# pro clf3
w <- t(clf3$coefs) %*% clf3$SV
slope <- - w[1] / w[2]
intercept <- clf3$rho / w[2]

df_lines <- rbind(df_lines,
                  data.frame(slope = slope,
                       intercept = intercept,
                       lb = intercept - 1 / w[2],
                       rb = intercept + 1 / w[2],
                       cost = C[3])
                  )

p3 <- p2 + 
  geom_abline(data = df_lines,
              aes(slope = slope, 
              intercept = intercept),
              col = 'grey2', linewidth = 0.7, alpha = 0.8) + 
  geom_abline(data = df_lines, 
              aes(slope = slope, 
              intercept = lb),
              col = 'grey2', linewidth = 0.5, alpha = 0.8,
              linetype = 'dashed') + 
  geom_abline(data = df_lines, 
              aes(slope = slope, 
              intercept = rb),
              col = 'grey2', linewidth = 0.5, alpha = 0.8,
              linetype = 'dashed') + 
  geom_point() + 
  geom_point(data = df_SV, col = 'grey2', alpha = 0.4,
                      size = 2) + 
  theme(legend.position = 'none')

p3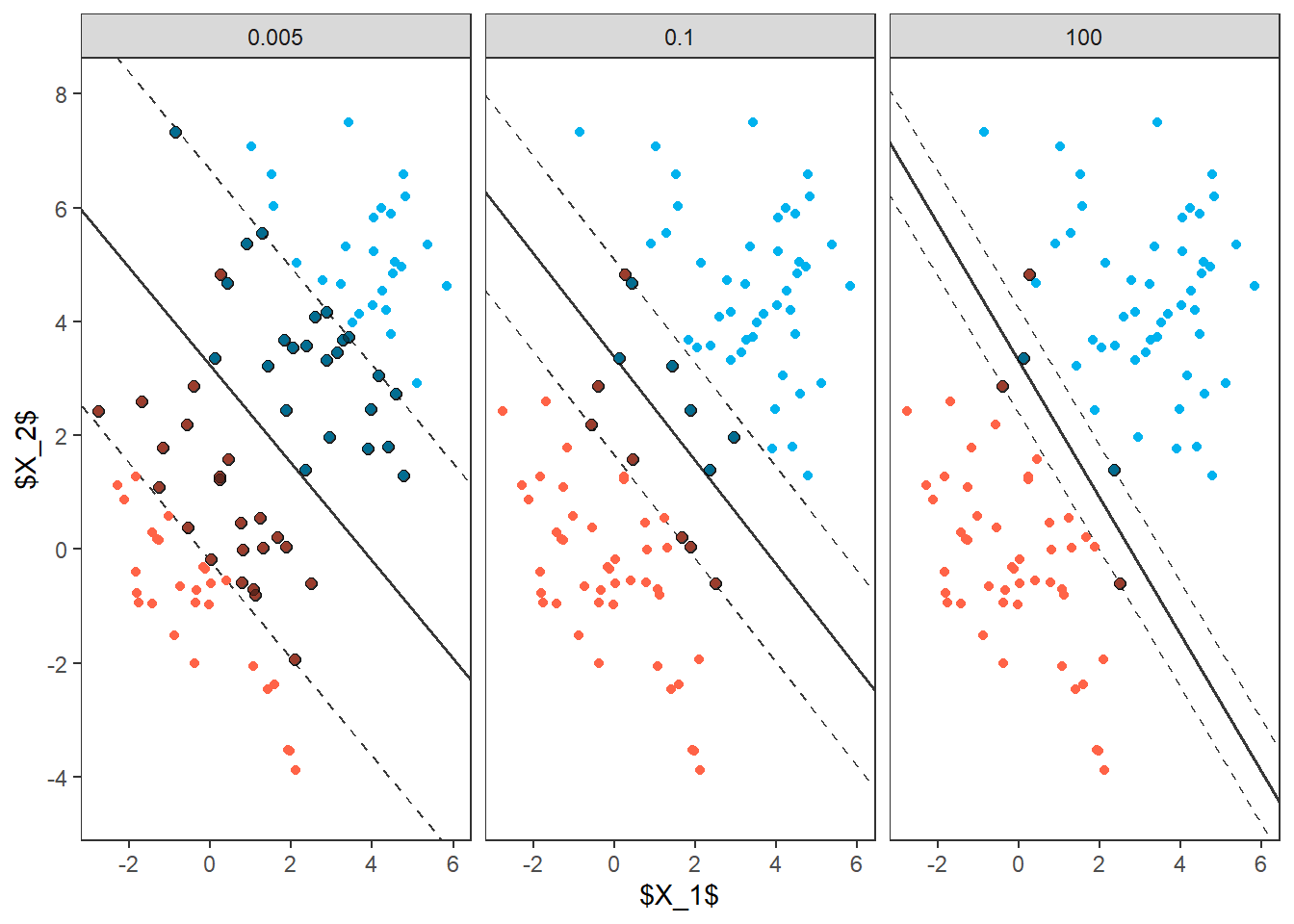

Code

# ggsave("figures/kap4_SVC_C_dependency.tex", device = tikz, width = 8, height = 3)

14.4.3 Support vector machines

Pro ilustraci této metody využijeme data tecator, kterým se podrobně věnujeme v Kapitole 11.

Code

# nacteni dat 
library(fda)
library(ggplot2)
library(dplyr)
library(tidyr)
library(ddalpha)

data <- ddalpha::dataf.tecator()

data.gr <- data$dataf[[1]]$vals
for(i in 2:length(data$labels)) {
  data.gr <- rbind(data.gr, data$dataf[[i]]$vals)
  }
data.gr <- cbind(data.frame(wave = data$dataf[[1]]$args),
                 t(data.gr))

# vektor trid
labels <- data$labels |> unlist()
# prejmenovani podle tridy
colnames(data.gr) <- c('wavelength',
                       paste0(labels, 1:length(data$labels)))

Code

t <- data.gr$wavelength
rangeval <- range(t)
breaks <- t
norder <- 6

bbasis <- create.bspline.basis(rangeval = rangeval, 
                               norder = norder, 
                               breaks = breaks)

curv.Lfd <- int2Lfd(4) # penalizujeme 4. derivaci

# spojeni pozorovani do jedne matice
XX <- data.gr[, -1] |> as.matrix()

lambda.vect <- 10^seq(from = -2, to = 1, length.out = 50) # vektor lambd
gcv <- rep(NA, length = length(lambda.vect)) # prazdny vektor pro ulozebi GCV

for(index in 1:length(lambda.vect)) {
  curv.Fdpar <- fdPar(bbasis, curv.Lfd, lambda.vect[index])
  BSmooth <- smooth.basis(t, XX, curv.Fdpar) # vyhlazeni
  gcv[index] <- mean(BSmooth$gcv) # prumer pres vsechny pozorovane krivky
}

GCV <- data.frame(
  lambda = round(log10(lambda.vect), 3),
  GCV = gcv
)

# najdeme hodnotu minima
lambda.opt <- lambda.vect[which.min(gcv)]

curv.fdPar <- fdPar(bbasis, curv.Lfd, lambda.opt)
BSmooth <- smooth.basis(t, XX, curv.fdPar)
XXfd <- BSmooth$fd

fdobjSmootheval <- eval.fd(fdobj = XXfd, evalarg = t)

# rozdeleni na testovaci a trenovaci cast
set.seed(42)
library(caTools)
split <- sample.split(XXfd$fdnames$reps, SplitRatio = 0.7)

# vytvoreni vektoru 0 a 1, 0 pro < 20 a 1 pro > 20 
Y <- ifelse(labels == 'large', 1, 0)

X.train <- subset(XXfd, split == TRUE)
X.test <- subset(XXfd, split == FALSE)

Y.train <- subset(Y, split == TRUE)
Y.test <- subset(Y, split == FALSE)

# vytvoreni vektoru 0 a 1, 0 pro < 20 a 1 pro > 20 
# Y <- ifelse(labels == 'large', 1, 0)
# X.train <- XXfd
# Y.train <- Y

# table(Y.train)
# 
# # relativni zastoupeni
# table(Y.train) / sum(table(Y.train))

Code

# analyza hlavnich komponent
data.PCA <- pca.fd(X.train, nharm = 10) # nharm - maximalni pocet HK
nharm <- which(cumsum(data.PCA$varprop) >= 0.9)[1] # urceni p
if(nharm == 1) nharm <- 2 # aby bylo mozne vykreslovat grafy,
# potrebujeme alespon 2 HK

data.PCA <- pca.fd(X.train, nharm = nharm) 
data.PCA.train <- as.data.frame(data.PCA$scores) # skore prvnich p HK
data.PCA.train$Y <- factor(Y.train) # prislusnost do trid

U všech třech jader projdeme hodnoty hyperparametru \(C\) v intervalu \([10^{-3}, 10^{3}]\), přičemž u jádra polynomiálního zafixujeme hyperparametr \(p\) na hodnotě 3, neboť pro jiné celočíselné hodnoty metoda nedává zdaleka tak dobré výsledky. Naopak pro radiální jádro využijeme k volbě optimální hodnoty hyperparametru \(\gamma\) opět 10-násobnou CV, přičemž uvažujeme hodnoty v intervalu \([10^{-3}, 10^{2}]\). Zvolíme coef0 \(= 1\).

Code

set.seed(42)
k_cv <- 10
# rozdelime trenovaci data na k casti
library(caret)
folds <- createMultiFolds(1:length(Y.train), k = k_cv, time = 1)

# ktere hodnoty gamma chceme uvazovat
gamma.cv <- 10^seq(-3, 2, length = 15)
C.cv <- 10^seq(-3, 3, length = 20)
p.cv <- c(2, 3, 4, 5)
coef0 <- 1

# list se tremi slozkami ... array pro jednotlive jadra -> linear, poly, radial
# prazdna matice, do ktere vlozime jednotlive vysledky
# ve sloupcich budou hodnoty presnosti pro dane
# v radcich budou hodnoty pro danou gamma a vrstvy odpovidaji folds
CV.results <- list(
  SVM.l = array(NA, dim = c(length(C.cv), k_cv)),
  SVM.p = array(NA, dim = c(length(C.cv), length(p.cv), k_cv)),
  SVM.r = array(NA, dim = c(length(C.cv), length(gamma.cv), k_cv))
)

# nejprve projdeme hodnoty C
for (C in C.cv) {
  # projdeme jednotlive folds
  for (index_cv in 1:k_cv) {
    # definice testovaci a trenovaci casti pro CV
    fold <- folds[[index_cv]]
    cv_sample <- 1:dim(data.PCA.train)[1] %in% fold
    
    data.PCA.train.cv <- as.data.frame(data.PCA.train[cv_sample, ])
    data.PCA.test.cv <- as.data.frame(data.PCA.train[!cv_sample, ])
    
    ## LINEARNI JADRO
    # sestrojeni modelu
    clf.SVM.l <- svm(Y ~ ., data = data.PCA.train.cv,
                     type = 'C-classification',
                     scale = TRUE,
                     cost = C,
                     kernel = 'linear')
    
    # presnost na validacnich datech
    predictions.test.l <- predict(clf.SVM.l, newdata = data.PCA.test.cv)
    presnost.test.l <- table(data.PCA.test.cv$Y, predictions.test.l) |>
      prop.table() |> diag() |> sum()
    
    # presnosti vlozime na pozice pro dane C a fold
    CV.results$SVM.l[(1:length(C.cv))[C.cv == C], 
                     index_cv] <- presnost.test.l
    
    ## POLYNOMIALNI JADRO
    for (p in p.cv) {
      # sestrojeni modelu
      clf.SVM.p <- svm(Y ~ ., data = data.PCA.train.cv,
                       type = 'C-classification',
                       scale = TRUE,
                       cost = C,
                       coef0 = coef0,
                       degree = p,
                       kernel = 'polynomial')
      
      # presnost na validacnich datech
      predictions.test.p <- predict(clf.SVM.p, newdata = data.PCA.test.cv)
      presnost.test.p <- table(data.PCA.test.cv$Y, predictions.test.p) |>
        prop.table() |> diag() |> sum()
      
      # presnosti vlozime na pozice pro dane C, p a fold
      CV.results$SVM.p[(1:length(C.cv))[C.cv == C], 
                       (1:length(p.cv))[p.cv == p],
                       index_cv] <- presnost.test.p
    }
        
    ## RADIALNI JADRO
    for (gamma in gamma.cv) {
      # sestrojeni modelu
      clf.SVM.r <- svm(Y ~ ., data = data.PCA.train.cv,
                       type = 'C-classification',
                       scale = TRUE,
                       cost = C,
                       gamma = gamma,
                       kernel = 'radial')
      
      # presnost na validacnich datech
      predictions.test.r <- predict(clf.SVM.r, newdata = data.PCA.test.cv)
      presnost.test.r <- table(data.PCA.test.cv$Y, predictions.test.r) |>
        prop.table() |> diag() |> sum()
      
      # presnosti vlozime na pozice pro dane C, gamma a fold
      CV.results$SVM.r[(1:length(C.cv))[C.cv == C], 
                       (1:length(gamma.cv))[gamma.cv == gamma],
                       index_cv] <- presnost.test.r
    }
  }
}

Nyní zprůměrujeme výsledky 10-násobné CV tak, abychom pro jednu hodnotu hyperparametru (případně jednu kombinaci hodnot) měli jeden odhad validační chybovosti. Přitom určíme i optimální hodnoty jednotlivých hyperparametrů.

Code

# spocitame prumerne presnosti pro jednotliva C pres folds
## Linearni jadro
CV.results$SVM.l <- apply(CV.results$SVM.l, 1, mean)
## Polynomialni jadro
CV.results$SVM.p <- apply(CV.results$SVM.p, c(1, 2), mean)
## Radialni jadro
CV.results$SVM.r <- apply(CV.results$SVM.r, c(1, 2), mean)

C.opt <- c(which.max(CV.results$SVM.l), 
           which.max(CV.results$SVM.p) %% length(C.cv), 
           which.max(CV.results$SVM.r) %% length(C.cv))
C.opt[C.opt == 0] <- length(C.cv)
C.opt <- C.cv[C.opt]

gamma.opt <- which.max(t(CV.results$SVM.r)) %% length(gamma.cv)
gamma.opt[gamma.opt == 0] <- length(gamma.cv)
gamma.opt <- gamma.cv[gamma.opt]

p.opt <- which.max(t(CV.results$SVM.p)) %% length(p.cv)
p.opt[p.opt == 0] <- length(p.cv)
p.opt <- p.cv[p.opt]

presnost.opt.cv <- c(max(CV.results$SVM.l), 
                     max(CV.results$SVM.p),
                     max(CV.results$SVM.r))

Code

# sestrojeni modelu
clf.SVM.l.PCA <- svm(Y ~ ., data = data.PCA.train,
                     type = 'C-classification',
                     scale = TRUE,
                     cost = C.opt[1],
                     kernel = 'linear')

clf.SVM.p.PCA <- svm(Y ~ ., data = data.PCA.train,
                     type = 'C-classification',
                     scale = TRUE,
                     cost = C.opt[2],
                     degree = p.opt,
                     coef0 = coef0,
                     kernel = 'polynomial')

clf.SVM.r.PCA <- svm(Y ~ ., data = data.PCA.train,
                     type = 'C-classification',
                     scale = TRUE,
                     cost = C.opt[3],
                     gamma = gamma.opt,
                     kernel = 'radial')

Code

# pridame diskriminacni hranici
np <- 1001 # pocet bodu site
# x-ova osa ... 1. HK
nd.x <- seq(from = min(data.PCA.train$V1) - 5, 
            to = max(data.PCA.train$V1) + 5, length.out = np)
# y-ova osa ... 2. HK
nd.y <- seq(from = min(data.PCA.train$V2) - 5, 
            to = max(data.PCA.train$V2) + 5, length.out = np)
# pripad pro 2 HK ... p = 2
nd <- expand.grid(V1 = nd.x, V2 = nd.y)

nd <- rbind(nd, nd, nd) |> mutate(
   prd = c(as.numeric(predict(clf.SVM.l.PCA, newdata = nd, type = 'response')),
           as.numeric(predict(clf.SVM.p.PCA, newdata = nd, type = 'response')),
           as.numeric(predict(clf.SVM.r.PCA, newdata = nd, type = 'response'))),
   kernel = rep(c('Lineární', 'Polynomiální', 'Radiální'),
                each = length(as.numeric(predict(clf.SVM.l.PCA, 
                                                 newdata = nd,
                                                 type = 'response')))) |>
     as.factor())

df_SV <- rbind(data.PCA.train[clf.SVM.l.PCA$index, ] |>
                 mutate(kernel = 'Lineární'),
               data.PCA.train[clf.SVM.p.PCA$index, ] |>
                 mutate(kernel = 'Polynomiální'),
               data.PCA.train[clf.SVM.r.PCA$index, ] |> 
                 mutate(kernel = 'Radiální'))

pSVM <- ggplot(data = data.PCA.train,
       aes(x = V1, y = V2, colour = Y)) +
  geom_contour(data = nd, aes(x = V1, y = V2, z = prd), 
              colour = 'grey2', size = 0.25) + 
  labs(x = '$X_1$',
       y = '$X_2$',
       colour = 'Klasifikační\n třída',
       fill = 'none') +
  scale_colour_manual(values = c('tomato', 'deepskyblue2')) + 
  theme_bw() +
  theme(panel.grid.major = element_blank(),
        panel.grid.minor = element_blank(),
        legend.title.align = 0.5,
        legend.position = 'none') + 
  scale_y_continuous(expand = c(-0.02, -0.02),
                     limits = c(-3.5, 2.5)) + 
  scale_x_continuous(expand = c(-0.02, -0.02),
                     limits = c(-15, 26)) + 
  facet_wrap(~kernel) + 
  geom_contour_filled(data = nd, aes(x = V1, y = V2, z = prd, colour = prd),
                      breaks = c(1, 2, 3), alpha = 0.1,
                      show.legend = F) +
  scale_fill_manual(values = c('tomato', 'deepskyblue2')) +
  geom_point(data = df_SV, col = 'grey2', alpha = 0.7,
                      size = 1.5) +
  geom_point(size = 1.2) + 
  geom_point(data = df_SV, col = 'grey2', alpha = 0.4,
                      size = 1.5)

pSVM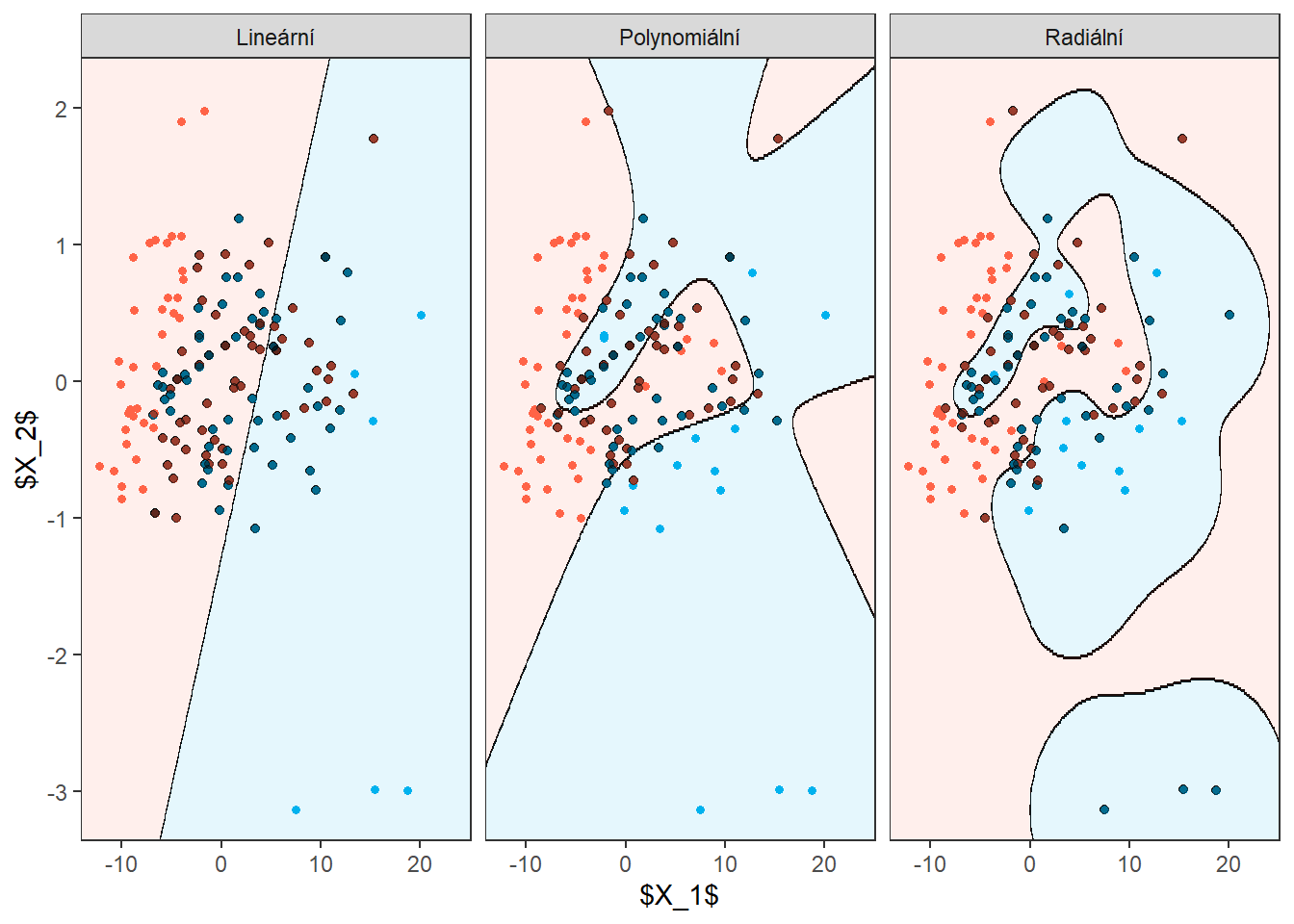

Skóre prvních dvou hlavních komponent, barevně odlišené podle příslušnosti do klasifikační třídy. Černě je vyznačena dělící hranice (přímka, resp. křivky v rovině prvních dvou hlavních komponent) mezi třídami sestrojená pomocí metody SVM.

Obrázek 9.1: Skóre prvních dvou hlavních komponent, barevně odlišené podle příslušnosti do klasifikační třídy. Černě je vyznačena dělící hranice (přímka, resp. křivky v rovině prvních dvou hlavních komponent) mezi třídami sestrojená pomocí metody SVM.

Code

# ggsave("figures/kap4_SVM.tex", device = tikz, width = 8, height = 3)

14.5 Materiály pro Kapitolu 5

V této sekci uvedeme podpůrné grafy pro pátou kapitolu diplomové práce.

14.5.1 Diskretizace intervalu

Chtěli bychom se podívat na hodnoty skalárních součinů funkcí, které jsou blízko u sebe a naopak které se tvarem velmi liší.

14.5.1.1 `tecator` data

Podívejme se také na data tecator.

Code

data <- ddalpha::dataf.tecator()

data.gr <- data$dataf[[1]]$vals
for(i in 2:length(data$labels)) {
  data.gr <- rbind(data.gr, data$dataf[[i]]$vals)
  }
data.gr <- cbind(data.frame(wave = data$dataf[[1]]$args),
                 t(data.gr))

# vektor trid
labels <- data$labels |> unlist()
# prejmenovani podle tridy
colnames(data.gr) <- c('wavelength',
                       paste0(labels, 1:length(data$labels)))

Code

library(fda.usc)
t <- data.gr$wavelength
rangeval <- range(t)
breaks <- t
norder <- 6

bbasis <- create.bspline.basis(rangeval = rangeval, 
                               norder = norder, 
                               breaks = breaks)

curv.Lfd <- int2Lfd(4) # penalizujeme 4. derivaci

# spojeni pozorovani do jedne matice
XX <- data.gr[, -1] |> as.matrix()

lambda.vect <- 10^seq(from = -2, to = 1, length.out = 50) # vektor lambd
gcv <- rep(NA, length = length(lambda.vect)) # prazdny vektor pro ulozebi GCV

for(index in 1:length(lambda.vect)) {
  curv.Fdpar <- fdPar(bbasis, curv.Lfd, lambda.vect[index])
  BSmooth <- smooth.basis(t, XX, curv.Fdpar) # vyhlazeni
  gcv[index] <- mean(BSmooth$gcv) # prumer pres vsechny pozorovane krivky
}

GCV <- data.frame(
  lambda = round(log10(lambda.vect), 3),
  GCV = gcv
)

# najdeme hodnotu minima
lambda.opt <- lambda.vect[which.min(gcv)]

curv.fdPar <- fdPar(bbasis, curv.Lfd, lambda.opt)
BSmooth <- smooth.basis(t, XX, curv.fdPar)
XXfd <- BSmooth$fd # * as.numeric(1 / norm.fd(BSmooth$fd[1]))
# set norm equal to one
norms <- c()
for (i in 1:215) {norms <- c(norms, as.numeric(1 / norm.fd(BSmooth$fd[i])))}
XXfd_norm <- XXfd 
XXfd_norm$coefs <- XXfd_norm$coefs * matrix(norms, ncol = 215, nrow = 104, byrow = T)

fdobjSmootheval <- eval.fd(fdobj = XXfd_norm, evalarg = t)

# rozdeleni na testovaci a trenovaci cast
set.seed(42)
library(caTools)
split <- sample.split(XXfd$fdnames$reps, SplitRatio = 0.7)

# vytvoreni vektoru 0 a 1, 0 pro < 20 a 1 pro > 20 
Y <- ifelse(labels == 'large', 1, 0)

X.train <- subset(XXfd, split == TRUE)
X.test <- subset(XXfd, split == FALSE)

Y.train <- subset(Y, split == TRUE)
Y.test <- subset(Y, split == FALSE)

# vytvoreni vektoru 0 a 1, 0 pro < 20 a 1 pro > 20 
# Y <- ifelse(labels == 'large', 1, 0)
# X.train <- XXfd
# Y.train <- Y

Spočítáme skalární součiny prvního s ostatními.

Code

n <- dim(XX)[2]
abs.labs <- c("$< 20 \\%$", "$> 20 \\%$")
# abs.labs <- c("$Y = {-1}$", "$Y = 1$")
names(abs.labs) <- c('small', 'large')

DFsmooth <- data.frame(
  t = rep(t, n),
  time = factor(rep(1:n, each = length(t))),
  Smooth = c(fdobjSmootheval),
  Fat = factor(rep(labels, each = length(t)), levels = c('small', 'large'))
)

DFmean <- data.frame(
  t = rep(t, 2),
  Mean = c(apply(fdobjSmootheval[ , labels == 'small'], 1, mean), 
            apply(fdobjSmootheval[ , labels == 'large'], 1, mean)),
  Fat = factor(rep(c('small', 'large'), each = length(t)),
                 levels = c('small', 'large'))
)

DFsmooth |> filter(time %in% as.character(c(nn))) |>
  ggplot(aes(x = t, y = Smooth, color = Fat)) +
  geom_line(linewidth = 1.1, aes(group = time, linetype = 'apozor x1')) +
  geom_line(data = DFsmooth |> 
              filter(time %in% as.character(order(Inprod_vect)[1:4])),
            aes(group = time, linetype = 'nejmensi'), linewidth = 0.6) +
  geom_line(data = DFsmooth |> 
              filter(time %in% as.character(rev(order(Inprod_vect))[1:5])),
            aes(group = time, linetype = 'nejvetsi'), linewidth = 0.6) +
  geom_line(linewidth = 1.1, aes(group = time, linetype = 'apozor x1')) +
  theme_bw() +
  # facet_wrap(~Fat,
  #            labeller = labeller(Fat = abs.labs)) + 
  labs(x = "Vlnová délka [v nm]",
       y = "Absorbance",
       colour = 'Obsah tuku',#"Klasifikační\n      třída",
       linetype = 'Styl čáry') + 
  # scale_color_discrete(guide="none") +
  scale_colour_manual(values = c('tomato', 'deepskyblue2'), labels = abs.labs) + 
  # guides(color = guide_legend(position = 'none')) +
  # scale_color_discrete(labels = abs.labs) +
  scale_linetype_manual(values=c('solid', "dotted", "longdash")) +
  theme(legend.position = c(0.15, 0.75),
        #legend.box="vertical",
        panel.grid = element_blank())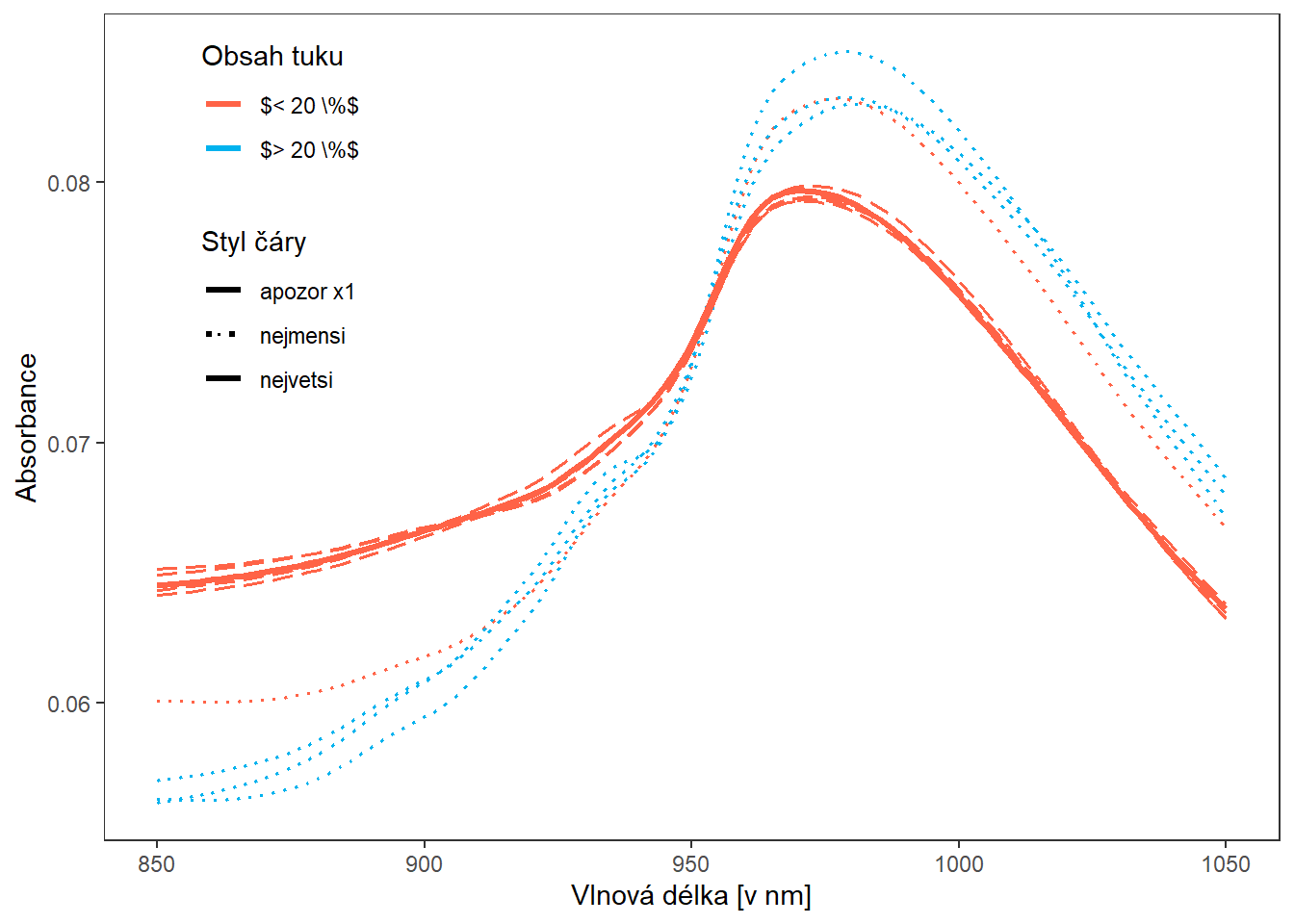

Obrázek 3.8: Vykreslení čtyř pozorování s minimální a maximální hodnotou skalárního součinu.

Code

# ggsave("figures/kap5_discretization_tecator.tex", device = tikz, width = 4.5, height = 4.5)

14.5.1.2 `phoneme` data

Použijeme data phoneme.

Code

library(fda.usc)
# nacteni dat
data <- read.delim2('phoneme.txt', header = T, sep = ',')

# zmenime dve promenne na typ factor
data <- data |> 
  mutate(g = factor(g),
         speaker = factor(speaker))

# numericke promenne prevedeme opravdu na numericke
data[, 2:257] <- as.numeric(data[, 2:257] |> as.matrix())

tr_vs_test <- str_split(data$speaker, '\\.') |> unlist()
tr_vs_test <- tr_vs_test[seq(1, length(tr_vs_test), by = 4)]
data$train <- ifelse(tr_vs_test == 'train', TRUE, FALSE)

# vybrane fonemy ke klasifikaci
phoneme_subset <- c('aa', 'ao')

# testovaci a trenovaci data
data_train <- data |> filter(train) |> filter(g %in% phoneme_subset)
data_test <- data |> filter(!train) |> filter(g %in% phoneme_subset)

# odstranime sloupce, ktere nenesou informaci o frekvenci a 
# transponujeme tak, aby ve sloupcich byly jednotlive zaznamy
X_train <- data_train[, -c(1, 258, 259, 260)] |> t()
X_test <- data_test[, -c(1, 258, 259, 260)] |> t()

# prejmenujeme radky a sloupce
rownames(X_train) <- 1:256
colnames(X_train) <- paste0('train', data_train$row.names)
rownames(X_test) <- 1:256
colnames(X_test) <- paste0('test', data_test$row.names)

# definujeme vektor fonemu
y_train <- data_train[, 258] |> factor(levels = phoneme_subset)
y_test <- data_test[, 258] |> factor(levels = phoneme_subset)
y <- c(y_train, y_test)

Code

t <- 1:256
rangeval <- range(t)
breaks <- t
norder <- 4

bbasis <- create.bspline.basis(rangeval = rangeval, 
                               norder = norder, 
                               breaks = breaks)

curv.Lfd <- int2Lfd(2) # penalizujeme 2. derivaci

# spojeni pozorovani do jedne matice
XX <- cbind(X_train, X_test) |> as.matrix()

lambda.vect <- 10^seq(from = 1, to = 3, length.out = 35) # vektor lambd
gcv <- rep(NA, length = length(lambda.vect)) # prazdny vektor pro ulozebi GCV

for(index in 1:length(lambda.vect)) {
  curv.Fdpar <- fdPar(bbasis, curv.Lfd, lambda.vect[index])
  BSmooth <- smooth.basis(t, XX, curv.Fdpar) # vyhlazeni
  gcv[index] <- mean(BSmooth$gcv) # prumer pres vsechny pozorovane krivky
}

GCV <- data.frame(
  lambda = round(log10(lambda.vect), 3),
  GCV = gcv
)

# najdeme hodnotu minima
lambda.opt <- lambda.vect[which.min(gcv)]

curv.fdPar <- fdPar(bbasis, curv.Lfd, lambda.opt)
BSmooth <- smooth.basis(t, XX, curv.fdPar)
XXfd <- BSmooth$fd

# set norm equal to one
norms <- c()
for (i in 1:dim(XXfd$coefs)[2]) {
  norms <- c(norms, as.numeric(1 / norm.fd(BSmooth$fd[i])))
  }
XXfd_norm <- XXfd 
XXfd_norm$coefs <- XXfd_norm$coefs * matrix(norms, 
                                            ncol = dim(XXfd$coefs)[2],
                                            nrow = dim(XXfd$coefs)[1],
                                            byrow = T)

fdobjSmootheval <- eval.fd(fdobj = XXfd_norm, evalarg = t)

Spočítáme skalární součiny prvního log-periodogramu s ostatními.

Code

n <- dim(XX)[2]
y <- c(y_train, y_test)
DFsmooth <- data.frame(
  t = rep(t, n),
  time = factor(rep(1:n, each = length(t))),
  Smooth = c(fdobjSmootheval),
  Phoneme = rep(y, each = length(t)))

DFmean <- data.frame(
  t = rep(t, 2),
  Mean = c(apply(fdobjSmootheval[ , y == phoneme_subset[1]], 1, mean),
            apply(fdobjSmootheval[ , y == phoneme_subset[2]], 1, mean)),
  Phoneme = factor(rep(phoneme_subset, each = length(t)),
                 levels = levels(y))
)

DFsmooth |> 
  filter(time %in% as.character(nn)) |>
  ggplot(aes(x = t, y = Smooth, color = Phoneme)) + 
  geom_line(linewidth = 1.1, aes(group = time, linetype = 'apozor x1')) +
  geom_line(data = DFsmooth |> 
              filter(time %in% as.character(order(Inprod_vect)[1:4])),
            aes(group = time, linetype = 'nejmensi'), linewidth = 0.6) +
  geom_line(data = DFsmooth |> 
              filter(time %in% as.character(rev(order(Inprod_vect))[1:5])),
            aes(group = time, linetype = 'nejvetsi'), linewidth = 0.6) +
  geom_line(linewidth = 1.1, aes(group = time, linetype = 'apozor x1')) +
  theme_bw() +
  labs(x = 'Frekvence',
       y = 'Log-periodogram',
       colour = 'Foném',
       linetype = 'Styl čáry') +
  # scale_colour_discrete(labels = phoneme_subset) +
  scale_colour_manual(values = c('tomato', 'deepskyblue2'),
                      labels = phoneme_subset) +
  scale_linetype_manual(values=c('solid', "dotted", "longdash")) +
  theme(legend.position = c(0.8, 0.75),
        panel.grid = element_blank())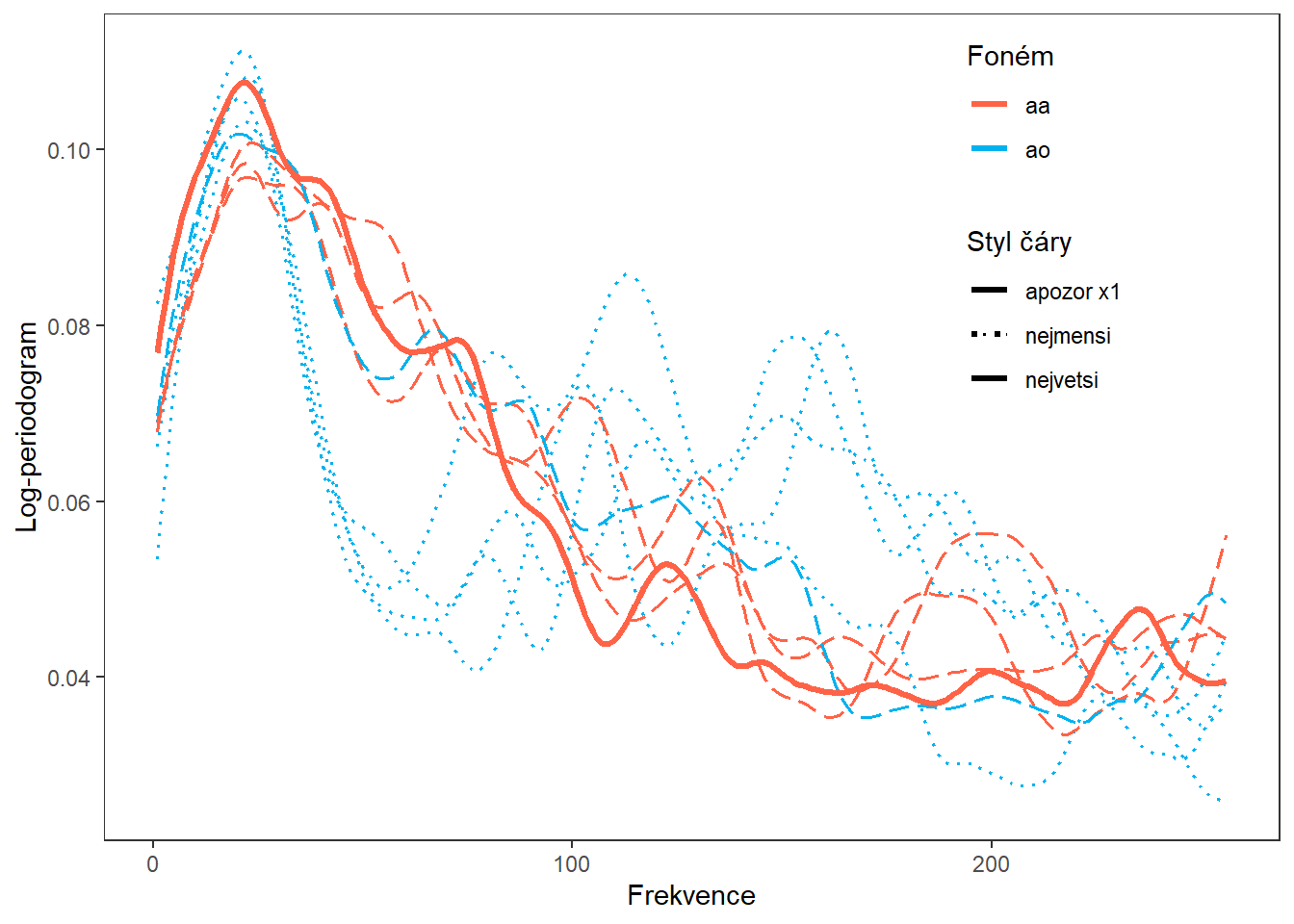

Obrázek 12.2: Vykreslení čtyř pozorování s minimální a maximální hodnotou skalárního součinu.

Code

# ggsave("figures/kap5_discretization_phoneme.tex", device = tikz, width = 4.5, height = 4.5)

14.5.2 Support vector regression (SVR)

Ukázka metody SVR na obou datových souborech.

14.5.2.1 `tecator` data

Code

t <- data.gr$wavelength
rangeval <- range(t)
breaks <- t
norder <- 6

bbasis <- create.bspline.basis(rangeval = rangeval, 
                               norder = norder, 
                               breaks = breaks)

curv.Lfd <- int2Lfd(4) # penalizujeme 4. derivaci

# spojeni pozorovani do jedne matice
XX <- data.gr[, -1] |> as.matrix()

lambda.vect <- 10^seq(from = -2, to = 1, length.out = 50) # vektor lambd
gcv <- rep(NA, length = length(lambda.vect)) # prazdny vektor pro ulozebi GCV

for(index in 1:length(lambda.vect)) {
  curv.Fdpar <- fdPar(bbasis, curv.Lfd, lambda.vect[index])
  BSmooth <- smooth.basis(t, XX, curv.Fdpar) # vyhlazeni
  gcv[index] <- mean(BSmooth$gcv) # prumer pres vsechny pozorovane krivky
}

GCV <- data.frame(
  lambda = round(log10(lambda.vect), 3),
  GCV = gcv
)

# najdeme hodnotu minima
lambda.opt <- lambda.vect[which.min(gcv)]

curv.fdPar <- fdPar(bbasis, curv.Lfd, lambda.opt)
BSmooth <- smooth.basis(t, XX, curv.fdPar)
XXfd <- BSmooth$fd 

fdobjSmootheval <- eval.fd(fdobj = XXfd, evalarg = t)

Code

library(e1071)
library(caret)

df_plot <- data.frame()

# model
for(i in 1:5) {
  df.svm <- data.frame(x = t,
                       y = fdobjSmootheval[, i])
  svm.RKHS <- svm(y ~ x, data = df.svm, 
                  kernel = 'radial',
                  type = 'eps-regression',
                  epsilon = 0.03,
                  gamma = 0.5,
                  cost = 1, 
                  tolerance = 0.001,
                  shrinking = TRUE,
                  scale = TRUE)
  
  svm.RKHS <- train(y ~ x, data = df.svm,
                    method = 'svmRadial',
                    metric = "RMSE",
                    preProcess = c('center', 'scale'),
                    trControl = trainControl(
                      method = "repeatedcv",
                      number = 10,
                      repeats = 10,
                      verboseIter = FALSE
                    )
                    # trControl = trainControl(method = "none"),
                    # Telling caret not to re-tune
                    # tuneGrid = data.frame(sigma = 1000, C = 1000)
                    # Specifying the parameters
                    )
  df_plot <- rbind(
    df_plot, 
    data.frame(
      x = t,
      y = svm.RKHS$finalModel@fitted * 
             svm.RKHS$finalModel@scaling$y.scale$`scaled:scale` +
             svm.RKHS$finalModel@scaling$y.scale$`scaled:center`,
      line = 'estimate',
      curve = as.character(i)) |>
      rbind(data.frame(
        x = t,
        y = fdobjSmootheval[, i],
        line = 'sample',
        curve = as.character(i)
  )))
}

Vykresleme si pro lepší představu odhad křivky (červeně) společně s pozorovanou křivkou (modře).

Code

df_plot |> filter(curve %in% c('1', '2', '3')) |> 
  ggplot(aes(x, y, col = line, linetype = curve)) +
  geom_line(linewidth = 0.8) + 
  theme_bw() +
  labs(x = "Vlnová délka [v nm]",
       y = "Absorbance",
       colour = 'Křivka') +
  # scale_colour_discrete(labels = phoneme_subset) +
  scale_colour_manual(values = c('tomato', 'deepskyblue2'),
                      labels = c("odhadnutá", "pozorovaná")) +
  scale_linetype_manual(values = c('solid', "dotted", "dashed")) +
  theme(legend.position = c(0.17, 0.85),
        panel.grid = element_blank()) + 
  guides(linetype = 'none')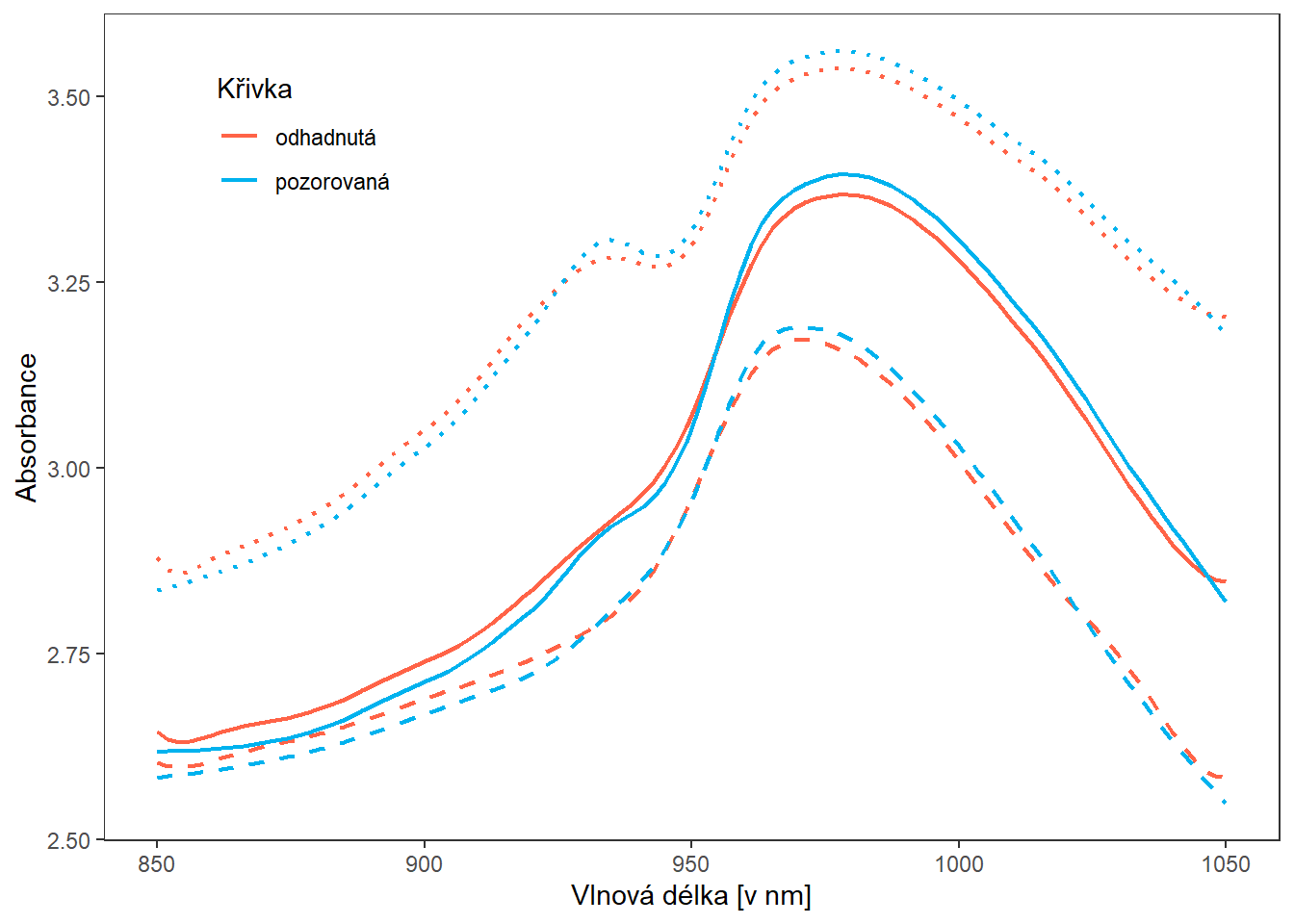

Obrázek 1.20: Porovnání pozorované a odhadnuté křivky.

Code

# ggsave("figures/kap5_SVR_tecator.tex", device = tikz, width = 4.5, height = 4.5)

14.5.2.2 `phoneme` data

Code

data <- read.delim2('phoneme.txt', header = T, sep = ',')

# zmenime dve promenne na typ factor
data <- data |> 
  mutate(g = factor(g),
         speaker = factor(speaker))

# numericke promenne prevedeme opravdu na numericke
data[, 2:257] <- as.numeric(data[, 2:257] |> as.matrix())

tr_vs_test <- str_split(data$speaker, '\\.') |> unlist()
tr_vs_test <- tr_vs_test[seq(1, length(tr_vs_test), by = 4)]
data$train <- ifelse(tr_vs_test == 'train', TRUE, FALSE)

# vybrane fonemy ke klasifikaci
phoneme_subset <- c('aa', 'ao')

# testovaci a trenovaci data
data_train <- data |> filter(train) |> filter(g %in% phoneme_subset)
data_test <- data |> filter(!train) |> filter(g %in% phoneme_subset)

# odstranime sloupce, ktere nenesou informaci o frekvenci a 
# transponujeme tak, aby ve sloupcich byly jednotlive zaznamy
X_train <- data_train[, -c(1, 258, 259, 260)] |> t()
X_test <- data_test[, -c(1, 258, 259, 260)] |> t()

# prejmenujeme radky a sloupce
rownames(X_train) <- 1:256
colnames(X_train) <- paste0('train', data_train$row.names)
rownames(X_test) <- 1:256
colnames(X_test) <- paste0('test', data_test$row.names)

# definujeme vektor fonemu
y_train <- data_train[, 258] |> factor(levels = phoneme_subset)
y_test <- data_test[, 258] |> factor(levels = phoneme_subset)
y <- c(y_train, y_test)

Code

t <- 1:256
rangeval <- range(t)
breaks <- t
norder <- 4

bbasis <- create.bspline.basis(rangeval = rangeval, 
                               norder = norder, 
                               breaks = breaks)

curv.Lfd <- int2Lfd(2) # penalizujeme 2. derivaci

# spojeni pozorovani do jedne matice
XX <- cbind(X_train, X_test) |> as.matrix()

lambda.vect <- 10^seq(from = 1, to = 3, length.out = 35) # vektor lambd
gcv <- rep(NA, length = length(lambda.vect)) # prazdny vektor pro ulozebi GCV

for(index in 1:length(lambda.vect)) {
  curv.Fdpar <- fdPar(bbasis, curv.Lfd, lambda.vect[index])
  BSmooth <- smooth.basis(t, XX, curv.Fdpar) # vyhlazeni
  gcv[index] <- mean(BSmooth$gcv) # prumer pres vsechny pozorovane krivky
}

GCV <- data.frame(
  lambda = round(log10(lambda.vect), 3),
  GCV = gcv
)

# najdeme hodnotu minima
lambda.opt <- lambda.vect[which.min(gcv)]

curv.fdPar <- fdPar(bbasis, curv.Lfd, lambda.opt)
BSmooth <- smooth.basis(t, XX, curv.fdPar)
XXfd <- BSmooth$fd

fdobjSmootheval <- eval.fd(fdobj = XXfd, evalarg = t)

Code

df_plot <- data.frame()
# model
for(i in 1:5) {
  df.svm <- data.frame(x = t,
                       y = fdobjSmootheval[, i])
  svm.RKHS <- svm(y ~ x, data = df.svm, 
                  kernel = 'radial',
                  type = 'eps-regression',
                  epsilon = 0.03,
                  gamma = 0.5,
                  cost = 1, 
                  tolerance = 0.001,
                  shrinking = TRUE,
                  scale = TRUE)
  
  svm.RKHS <- train(y ~ x, data = df.svm,
                    method = 'svmRadial',
                    metric = "RMSE",
                    preProcess = c('center', 'scale'),
                    trControl = trainControl(
                      method = "repeatedcv",
                      number = 10,
                      repeats = 10,
                      verboseIter = FALSE
                    )
                    # trControl = trainControl(method = "none"),
                    # Telling caret not to re-tune
                    # tuneGrid = data.frame(sigma = 1000, C = 1000)
                    # Specifying the parameters
                    )
  df_plot <- rbind(
    df_plot, 
    data.frame(
      x = t,
      y = svm.RKHS$finalModel@fitted * 
             svm.RKHS$finalModel@scaling$y.scale$`scaled:scale` +
             svm.RKHS$finalModel@scaling$y.scale$`scaled:center`,
      line = 'estimate',
      curve = as.character(i)) |>
      rbind(data.frame(
        x = t,
        y = fdobjSmootheval[, i],
        line = 'sample',
        curve = as.character(i)
  )))
}

Vykresleme si pro lepší představu odhad křivky (červeně) společně s pozorovanou křivkou (modře).

Code

df_plot |> filter(curve %in% c('1', '5', '3')) |> 
  ggplot(aes(x, y, col = line, linetype = curve)) +
  geom_line(linewidth = 0.8) + 
  theme_bw() +
  labs(x = 'Frekvence',
       y = 'Log-periodogram',
       colour = 'Křivka') +
  # scale_colour_discrete(labels = phoneme_subset) +
  scale_colour_manual(values = c('tomato', 'deepskyblue2'),
                      labels = c("odhadnutá", "pozorovaná")) +
  scale_linetype_manual(values = c('solid', "dotted", "dashed")) +
  theme(legend.position = c(0.8, 0.85),
        panel.grid = element_blank()) + 
  guides(linetype = 'none')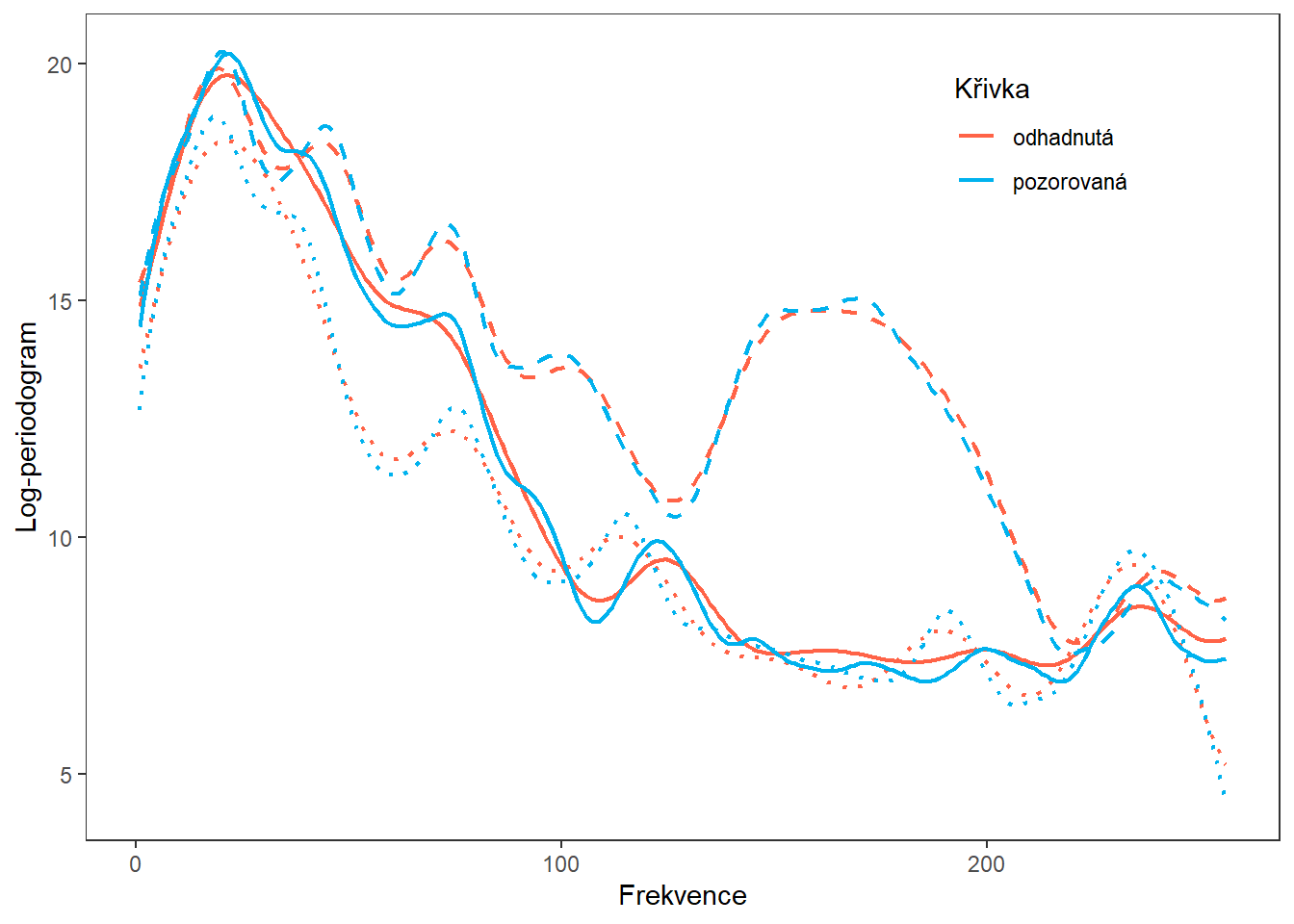

Obrázek 9.2: Porovnání pozorované a odhadnuté křivky.

Code

# ggsave("figures/kap5_SVR_phoneme.tex", device = tikz, width = 4.5, height = 4.5)

14.6 Materiály pro Kapitolu 6

Veškeré grafické podklady i číselné výstupy prezentované v Diplomové práci v Kapitole 6 jsou k dispozici v Kapitole 5 (případně také v Kapitolách 6, 7 a 8) a v Kapitole 9. Krabicové diagramy testovacích chybovostí jsme vizuálně upravili pro potřeby diplomové práce (barevnost, změna měřítka, popisky), kód použitý k jejich vygenerování je k vidění v příslušných buňkách (zapoznámkovaný).

14.7 Materiály pro Kapitolu 7

Veškeré grafické podklady i číselné výstupy prezentované v Diplomové práci v Kapitole 7 jsou k dispozici v Kapitole 11, která je věnována datovému souboru phoneme, a Kapitole 12 věnované datovému souboru tecator. Krabicové diagramy testovacích chybovostí jsme vizuálně upravili pro potřeby diplomové práce (barevnost, změna měřítka, popisky), kód použitý k jejich vygenerování je k vidění v příslušných buňkách (zapoznámkovaný).

Kapitola 14 Podpůrné materiály pro diplomovou práci

14.1 Materiály pro Kapitolu 1

14.1.1 Funkcionální průměr

14.1.2 Variance

14.1.3 Kovariance a Korelace

14.1.4 B-splinová báze

14.1.4.1 pro norder = 2

14.1.4.2 pro norder = 4

14.1.5 Fourierova báze

14.1.5.1 pro nbasis = 5

14.1.5.2 pro nbasis = 7

14.2 Materiály pro Kapitolu 2

14.2.1 Počet bázových funkcí a výsledný odhad

14.2.2 Volba \(\lambda\)

14.2.3 Vyhlazení s optimální \(\lambda\)

14.2.4 Funkcionální PCA

14.3 Materiály pro Kapitolu 3

14.4 Materiály pro Kapitolu 4

14.4.1 Maximal margin classifier

14.4.2 Support vector classifier

14.4.2.1 Změna šířky tolerančního pásma při změně hyperparametru \(C\)

14.4.3 Support vector machines

14.5 Materiály pro Kapitolu 5

14.5.1 Diskretizace intervalu

14.5.1.1 tecator data

14.5.1.2 phoneme data

14.5.2 Support vector regression (SVR)

14.5.2.1 tecator data

14.5.2.2 phoneme data

14.6 Materiály pro Kapitolu 6

14.7 Materiály pro Kapitolu 7

14.1.4.1 pro `norder = 2`

14.1.4.2 pro `norder = 4`

14.1.5.1 pro `nbasis = 5`

14.1.5.2 pro `nbasis = 7`

14.5.1.1 `tecator` data

14.5.1.2 `phoneme` data

14.5.2.1 `tecator` data

14.5.2.2 `phoneme` data