Kapitola 8 Závislost na diskretizaci

V této části se budeme zabývat závislostí výsledků z předchozí sekce 5 na hodnotě \(p\), která definuje délku ekvidistantní posloupnosti bodů, které jsou použity k diskretizaci pozorovaných funkcionálních objektů. Bude nás zajímat, jak se mění chybovosti jednotlivých klasifikačních metod při zjemňování dělení intervalu, tedy při zvětšující se dimenzi diskretizovaných vektorů.

Naším předpokladem je, že metoda podpůrných vektorů aplikovaná na diskretizovaná data by měla při zvětšujícím se \(p\) dávat menší chybovosti, neboť lépe aproximujeme integrály a tedy hodnoty jádrových funkcí funkcionálních analogií. Naopak bychom čekali, že rozhodovací stromy i náhodné lesy budou od jistého počtu \(p\) stagnovat.

Jelikož se bavíme o diskretizaci intervalu, v této Kapitole se budeme zabývat pouze metodami pracujícími s diskretizovanými daty – tedy metodami:

• Rozhodovací strom,
• Náhodný les,
• metoda SVM.

Kromě průměrné testovací chybovosti by nás také zajímala časová náročnost jednotlivých metod při zvětšující se hodnotě \(p\), neboť minimální chybovost není v praxi jediné kritérium pro použití dané klasifikační metody. Poměrně důležitou roli hraje právě i výpočetní obtížnost a s ní spojená časová náročnost.

Tato kapitola sestává ze dvou částí. V první Sekci 8.3 zvolíme pevný počet \(p=101\) diskretizovaných hodnot a podíváme se na jednotlivé metody, jejich chybovost i časovou náročnost. Následně V Sekci 8.4 definujeme posloupnost hodnot \(p\) a pro každou několikrát celý proces zopakujeme tak, abychom mohli stanovit pro tuto hodnotu průměrné výsledky. Nakonec si vykreslíme závislost chybovosti a časové náročnosti na hodnotě \(p\) počtu bodů.

8.1 Simulace funkcionálních dat

Nejprve si simulujeme funkce, které budeme následně chtít klasifikovat. Budeme uvažovat pro jednoduchost dvě klasifikační třídy. Pro simulaci nejprve:

• zvolíme vhodné funkce,
• generujeme body ze zvoleného intervalu, které obsahují, například gaussovský, šum,
• takto získané diskrétní body vyhladíme do podoby funkcionálního objektu pomocí nějakého vhodného bázového systému.

Tímto postupem získáme funkcionální objekty společně s hodnotou kategoriální proměnné \(Y\), která rozlišuje příslušnost do klasifikační třídy.

Code

# nacteme potrebne balicky 

library(fda)
library(ggplot2)
library(dplyr)
library(tidyr)
library(ddalpha)
library(polynom)

set.seed(42)

Uvažujme tedy dvě klasifikační třídy, \(Y \in \{0, 1\}\), pro každou ze tříd stejný počet n generovaných funkcí. Definujme si nejprve dvě funkce, každá bude pro jednu třídu. Funkce budeme uvažovat na intervalu \(I = [0, 6]\).

Nyní vytvoříme funkce pomocí interpolačních polynomů. Nejprve si definujeme body, kterými má procházet naše křivka, a následně jimi proložíme interpolační polynom, který použijeme pro generování křivek pro klasifikaci.

Code

# definujici body pro tridu 0
x.0 <- c(0.00, 0.65, 0.94, 1.42, 2.26, 2.84, 3.73, 4.50, 5.43, 6.00)
y.0 <- c(0, 0.25, 0.86, 1.49, 1.1, 0.15, -0.11, -0.36, 0.23, 0)

# definujici body pro tridu 1
x.1 <- c(0.00, 0.51, 0.91, 1.25, 1.51, 2.14, 2.43, 2.96, 3.70, 4.60,
         5.25, 5.67, 6.00)
y.1 <- c(0.1, 0.4, 0.71, 1.08, 1.47, 1.39, 0.81, 0.05, -0.1, -0.4,
         0.3, 0.37, 0)

Code

# graf bodu
dat_points <- data.frame(x = c(x.0, x.1),
                         y = c(y.0, y.1),
                         Class = rep(c('Y = 0', 'Y = 1'), 
                                     c(length(x.0), length(x.1))))

ggplot(dat_points, aes(x = x, y = y, colour = Class)) + 
  geom_point(size=1.5) + 
  theme_bw() + 
  labs(colour = 'Klasifikační\n      třída')

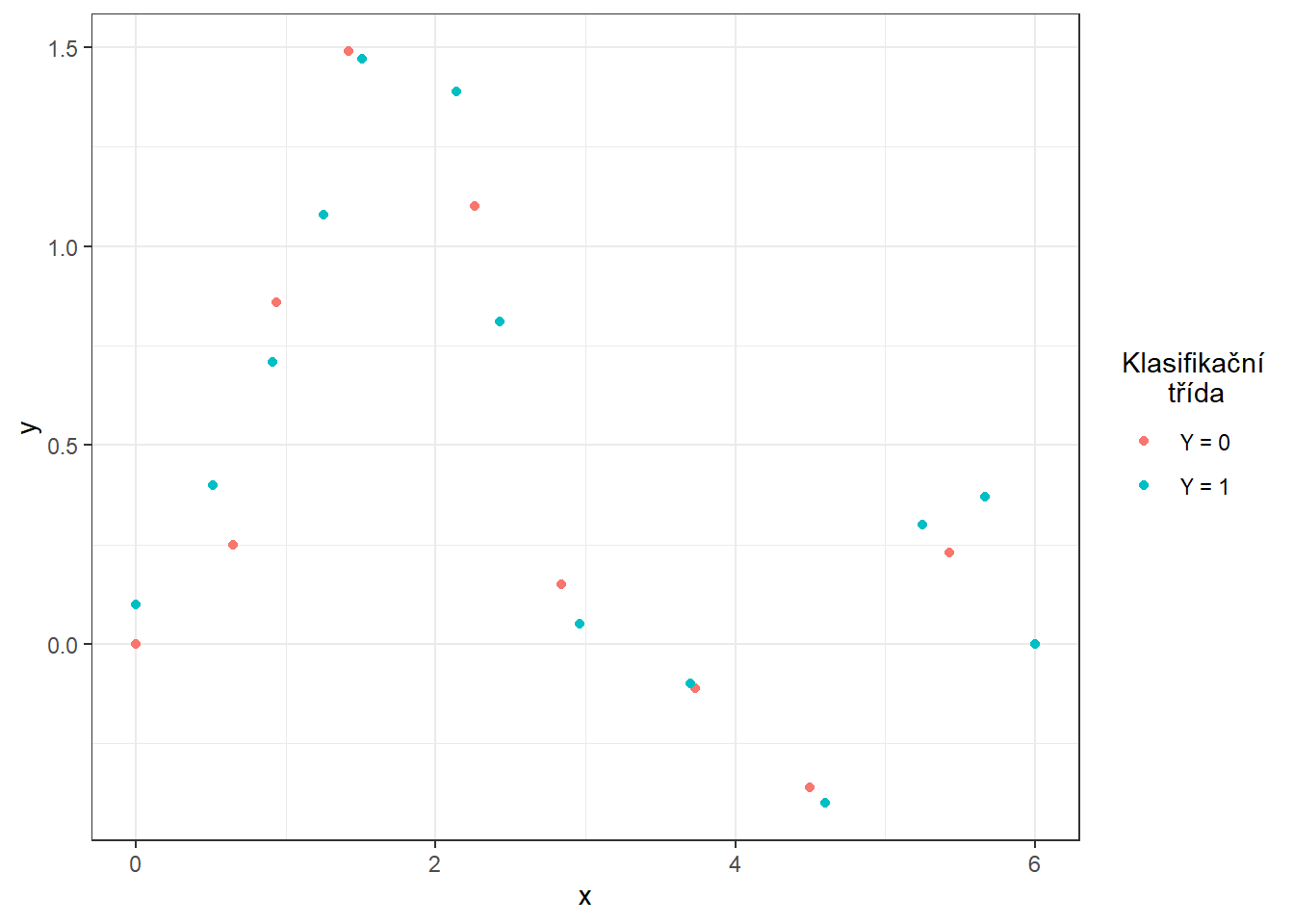
Obrázek 1.1: Body definující interpolační polynomy.

Pro výpočet interpolačních polynomů využijeme funkci poly.calc() z knihovny polynom. Dále definujeme funkce poly.0() a poly.1(), které budou počítat hodnoty polynomů v daném bodě intervalu. K jejich vytvoření použijeme funkci predict(), na jejíž vstup zadáme příslušný polynom a bod, ve kterám chceme polynom vyhodnotit.

Code

# vypocet polynomu
polynom.0 <- poly.calc(x.0, y.0)
polynom.1 <- poly.calc(x.1, y.1)

Code

poly.0 <- function(x) return(predict(polynom.0, x))
poly.1 <- function(x) return(predict(polynom.1, x))

Code

# vykresleni polynomu
xx <- seq(min(x.0), max(x.0), length = 501)
yy.0 <- poly.0(xx)
yy.1 <- poly.1(xx)

dat_poly_plot <- data.frame(x = c(xx, xx),
                            y = c(yy.0, yy.1),
                            Class = rep(c('Y = 0', 'Y = 1'), 
                                        c(length(xx), length(xx))))

ggplot(dat_points, aes(x = x, y = y, colour = Class)) + 
  geom_point(size=1.5) + 
  theme_bw() + 
  geom_line(data = dat_poly_plot,
            aes(x = x, y = y, colour = Class),
            linewidth = 0.8) + 
  labs(colour = 'Klasifikační\n      třída')

Obrázek 1.2: Znázornění dvou funkcí na intervalu \(I = [0, 6]\), ze kterých generujeme pozorování ze tříd 0 a 1.

Code

# generujici funkce pro Y = 0 a Y = 1
funkce_0 <- poly.0
funkce_1 <- poly.1

Nyní si vytvoříme funkci pro generování náhodných funkcí s přidaným šumem (resp. bodů na předem dané síti) ze zvolené generující funkce. Argument t označuje vektor hodnot, ve kterých chceme dané funkce vyhodnotit, fun značí generující funkci, n počet funkcí a sigma směrodatnou odchylku \(\sigma\) normálního rozdělení \(\text{N}(\mu, \sigma^2)\), ze kterého náhodně generujeme gaussovský bílý šum s \(\mu = 0\). Abychom ukázali výhodu použití metod, které pracují s funkcionálními daty, přidáme při generování ke každému simulovanému pozorování navíc i náhodný člen, který bude mít význam vertikálního posunu celé funkce (parametr sigma_shift). Tento posun budeme generovat s normálního rozdělení s parametrem \(\sigma^2 = 4\).

Code

generate_values <- function(t, fun, n, sigma, sigma_shift = 0) {
  # Arguments:
  # t ... vector of values, where the function will be evaluated
  # fun ... generating function of t 
  # n ... the number of generated functions / objects
  # sigma ... standard deviation of normal distribution to add noise to data
  # sigma_shift ... parameter of normal distribution for generating shift
  
  # Value:
  # X ... matrix of dimension length(t) times n with generated values of one 
  # function in a column 
  
  X <- matrix(rep(t, times = n), ncol = n, nrow = length(t), byrow = FALSE)
  noise <- matrix(rnorm(n * length(t), mean = 0, sd = sigma),
                  ncol = n, nrow = length(t), byrow = FALSE)
  shift <- matrix(rep(rnorm(n, 0, sigma_shift), each = length(t)),
                  ncol = n, nrow = length(t))
  return(fun(X) + noise + shift)
}

Nyní můžeme generovat funkce. V každé ze dvou tříd budeme uvažovat 100 pozorování, tedy n = 100.

Code

# pocet vygenerovanych pozorovani pro kazdou tridu
n <- 100
# vektor casu ekvidistantni na intervalu [0, 6]
t <- seq(0, 6, length = 51)

# pro Y = 0
X0 <- generate_values(t, funkce_0, n, 1, 2)
# pro Y = 1
X1 <- generate_values(t, funkce_1, n, 1, 2)

Vykreslíme vygenerované (ještě nevyhlazené) funkce barevně v závislosti na třídě (pouze prvních 10 pozorování z každé třídy pro přehlednost).

Code

n_curves_plot <- 10 # pocet krivek, ktere chceme vykreslit z kazde skupiny

DF0 <- cbind(t, X0[, 1:n_curves_plot]) |> 
  as.data.frame() |> 
  reshape(varying = 2:(n_curves_plot + 1), direction = 'long', sep = '') |> 
  subset(select = -id) |> 
  mutate(
  time = time - 1,
  group = 0
  )

DF1 <- cbind(t, X1[, 1:n_curves_plot]) |> 
  as.data.frame() |> 
  reshape(varying = 2:(n_curves_plot + 1), direction = 'long', sep = '') |> 
  subset(select = -id) |> 
  mutate(
  time = time - 1,
  group = 1
  )

DF <- rbind(DF0, DF1) |>
  mutate(group = factor(group))

DF |> ggplot(aes(x = t, y = V, group = interaction(time, group), 
                 colour = group)) + 
  geom_line(linewidth = 0.5) +
  theme_bw() +
  labs(x = expression(x[1]),
       y = expression(x[2]),
       colour = 'Klasifikační\n      třída') +
  scale_colour_discrete(labels=c('Y = 0', 'Y = 1'))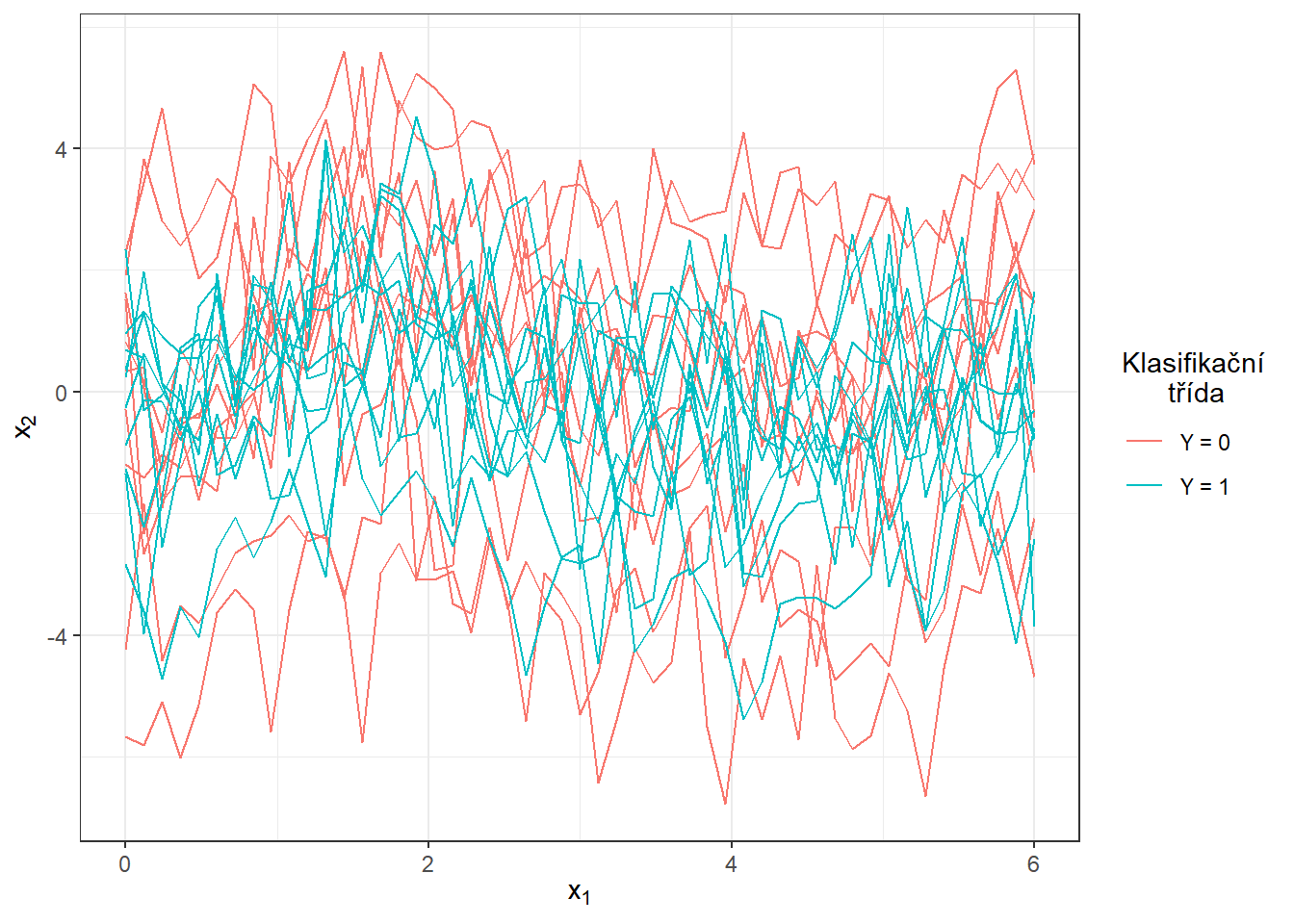

Obrázek 1.4: Prvních 10 vygenerovaných pozorování z každé ze dvou klasifikačních tříd. Pozorovaná data nejsou vyhlazená.

8.2 Vyhlazení pozorovaných křivek

Nyní převedeme pozorované diskrétní hodnoty (vektory hodnot) na funkcionální objekty, se kterými budeme následně pracovat. Opět využijeme k vyhlazení B-sline bázi.

Za uzly bereme celý vektor t, standardně uvažujeme kubické spliny, proto volíme (implicitní volba v R) norder = 4. Budeme penalizovat druhou derivaci funkcí.

Code

rangeval <- range(t)
breaks <- t
norder <- 4

bbasis <- create.bspline.basis(rangeval = rangeval, 
                               norder = norder, 
                               breaks = breaks)

curv.Lfd <- int2Lfd(2) # penalizujeme 2. derivaci

Najdeme vhodnou hodnotu vyhlazovacího parametru \(\lambda > 0\) pomocí \(GCV(\lambda)\), tedy pomocí zobecněné cross–validace. Hodnotu \(\lambda\) budeme uvažovat pro obě klasifikační skupiny stejnou, neboť pro testovací pozorování bychom dopředu nevěděli, kterou hodnotu \(\lambda\), v případě rozdílné volby pro každou třídu, máme volit.

Code

# spojeni pozorovani do jedne matice
XX <- cbind(X0, X1)

lambda.vect <- 10^seq(from = -2, to = 1, length.out = 50) # vektor lambd
gcv <- rep(NA, length = length(lambda.vect)) # prazdny vektor pro ulozebi GCV

for(index in 1:length(lambda.vect)) {
  curv.Fdpar <- fdPar(bbasis, curv.Lfd, lambda.vect[index])
  BSmooth <- smooth.basis(t, XX, curv.Fdpar) # vyhlazeni
  gcv[index] <- mean(BSmooth$gcv) # prumer pres vsechny pozorovane krivky
}

GCV <- data.frame(
  lambda = round(log10(lambda.vect), 3),
  GCV = gcv
)

# najdeme hodnotu minima
lambda.opt <- lambda.vect[which.min(gcv)]

Pro lepší znázornění si vykreslíme průběh \(GCV(\lambda)\).

Code

GCV |> ggplot(aes(x = lambda, y = GCV)) + 
  geom_line(linetype = 'solid', linewidth = 0.6) + 
  geom_point(size = 1.5) + 
  theme_bw() + 
  labs(x = bquote(paste(log[10](lambda), ' ;   ', 
                        lambda[optimal] == .(round(lambda.opt, 4)))),
       y = expression(GCV(lambda))) + 
  geom_point(aes(x = log10(lambda.opt), y = min(gcv)), colour = 'red', size = 2.5)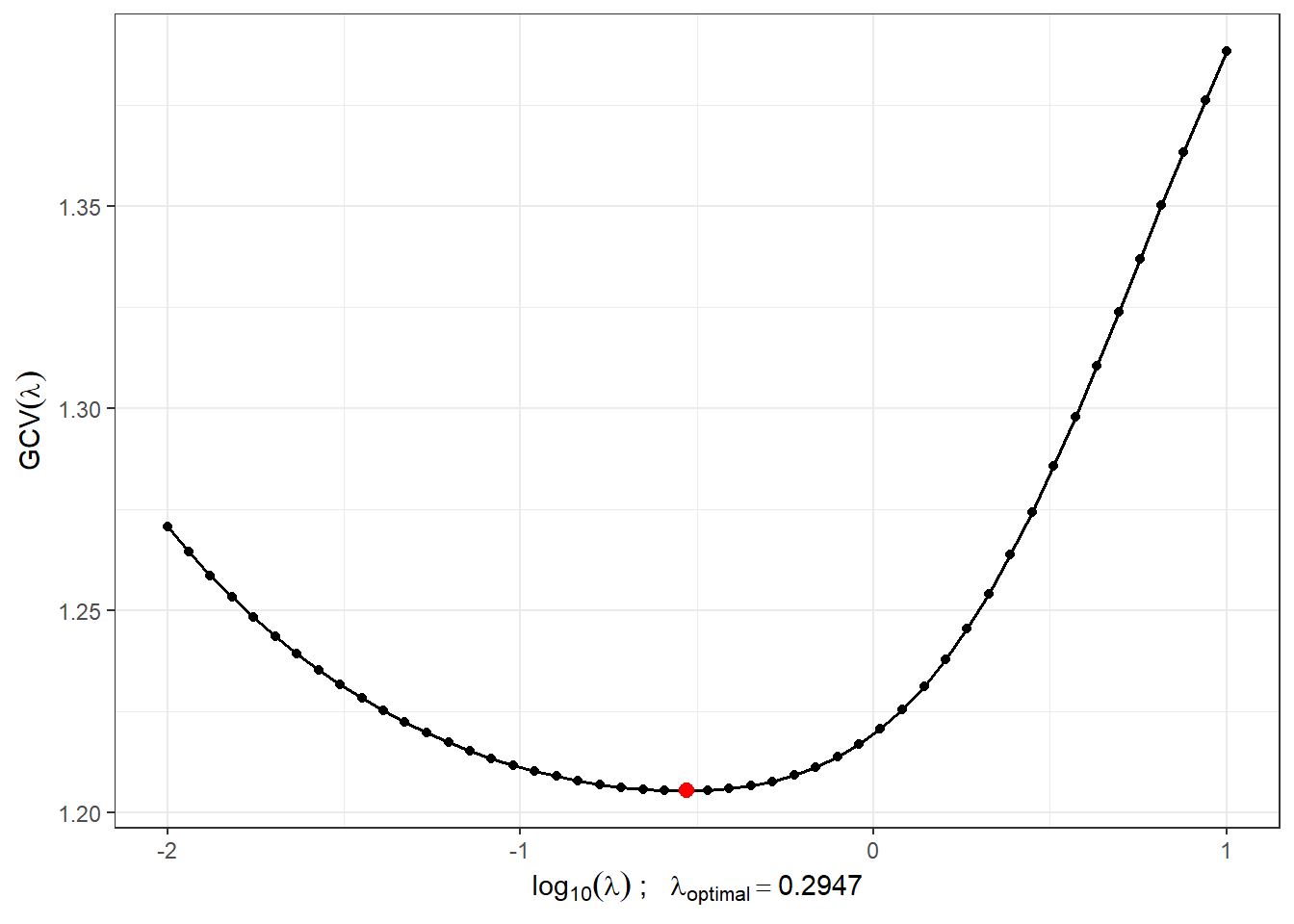

Obrázek 2.2: Průběh \(GCV(\lambda)\) pro zvolený vektor \(\boldsymbol\lambda\). Na ose \(x\) jsou hodnoty vyneseny v logaritmické škále. Červeně je znázorněna optimální hodnota vyhlazovacího parametru \(\lambda_{optimal}\).

S touto optimální volbou vyhlazovacího parametru \(\lambda\) nyní vyhladíme všechny funkce a opět znázorníme graficky prvních 10 pozorovaných křivek z každé klasifikační třídy.

Code

curv.fdPar <- fdPar(bbasis, curv.Lfd, lambda.opt)
BSmooth <- smooth.basis(t, XX, curv.fdPar)
XXfd <- BSmooth$fd

fdobjSmootheval <- eval.fd(fdobj = XXfd, evalarg = t)
DF$Vsmooth <- c(fdobjSmootheval[, c(1 : n_curves_plot, 
                                    (n + 1) : (n + n_curves_plot))])

DF |> ggplot(aes(x = t, y = Vsmooth, group = interaction(time, group), 
                 colour = group)) + 
  geom_line(linewidth = 0.75) +
  theme_bw() +
  labs(x = expression(x[1]),
       y = expression(x[2]),
       colour = 'Klasifikační\n      třída') +
  scale_colour_discrete(labels=c('Y = 0', 'Y = 1'))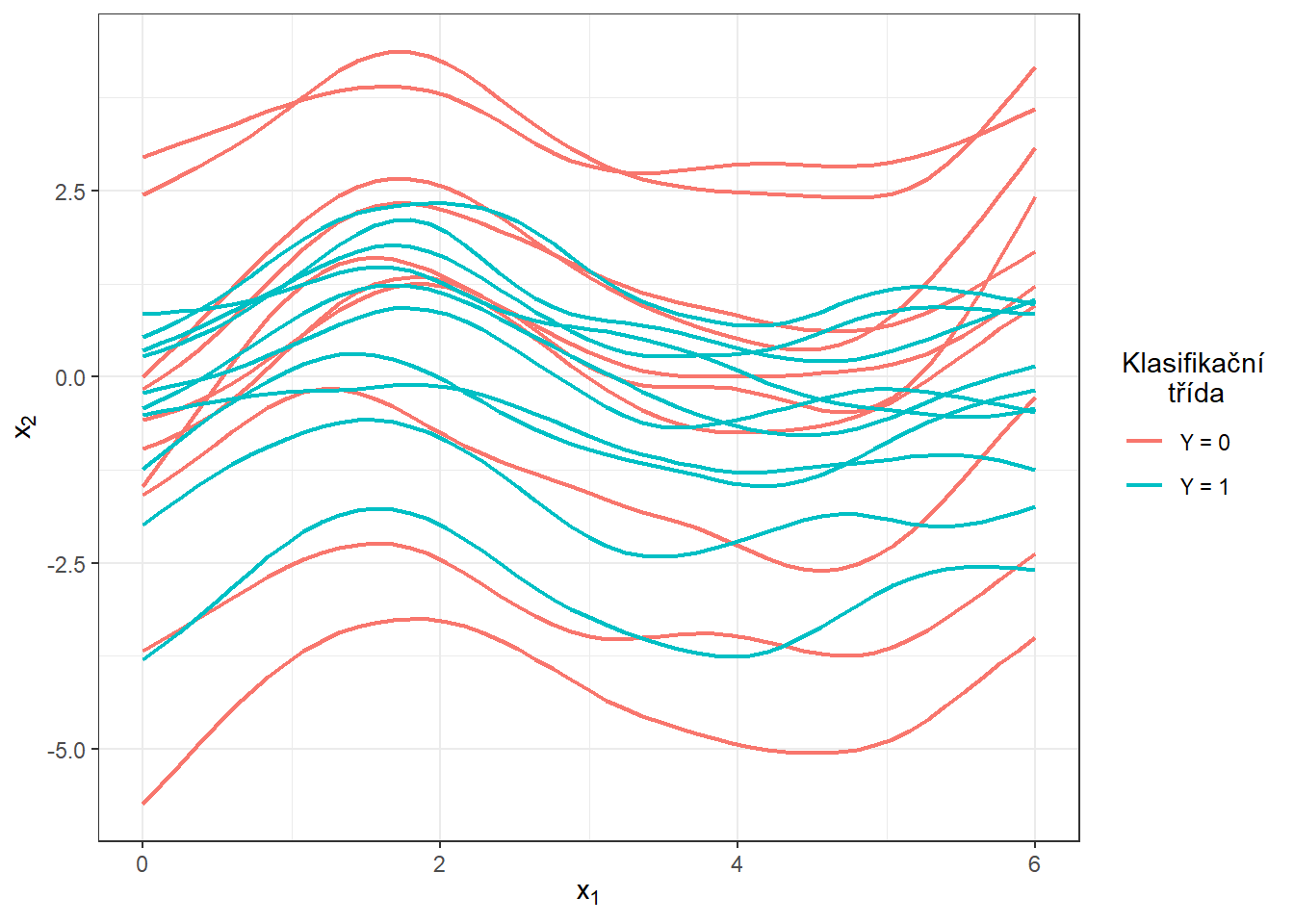

Obrázek 2.3: Prvních 10 vyhlazených křivek z každé klasifikační třídy.

Ještě znázorněme všechny křivky včetně průměru zvlášť pro každou třídu.

Code

DFsmooth <- data.frame(
  t = rep(t, 2 * n),
  time = rep(rep(1:n, each = length(t)), 2),
  Smooth = c(fdobjSmootheval),
  Mean = c(rep(apply(fdobjSmootheval[ , 1 : n], 1, mean), n),
            rep(apply(fdobjSmootheval[ , (n + 1) : (2 * n)], 1, mean), n)),
  group = factor(rep(c(0, 1), each = n * length(t)))
)

DFmean <- data.frame(
  t = rep(t, 2),
  Mean = c(apply(fdobjSmootheval[ , 1 : n], 1, mean), 
            apply(fdobjSmootheval[ , (n + 1) : (2 * n)], 1, mean)),
  group = factor(rep(c(0, 1), each = length(t)))
)

DFsmooth |> ggplot(aes(x = t, y = Smooth, group = interaction(time, group), 
                 colour = group)) + 
  geom_line(linewidth = 0.25, alpha = 0.5) +
  theme_bw() +
  labs(x = expression(x[1]),
       y = expression(x[2]),
       colour = 'Klasifikační\n      třída') +
  scale_colour_discrete(labels = c('Y = 0', 'Y = 1')) + 
  geom_line(aes(x = t, y = Mean, colour = group), 
            linewidth = 1.2, linetype = 'solid') + 
  scale_x_continuous(expand = c(0.01, 0.01)) + 
  #ylim(c(-1, 2)) + 
  scale_y_continuous(expand = c(0.01, 0.01))#, limits = c(-1, 2))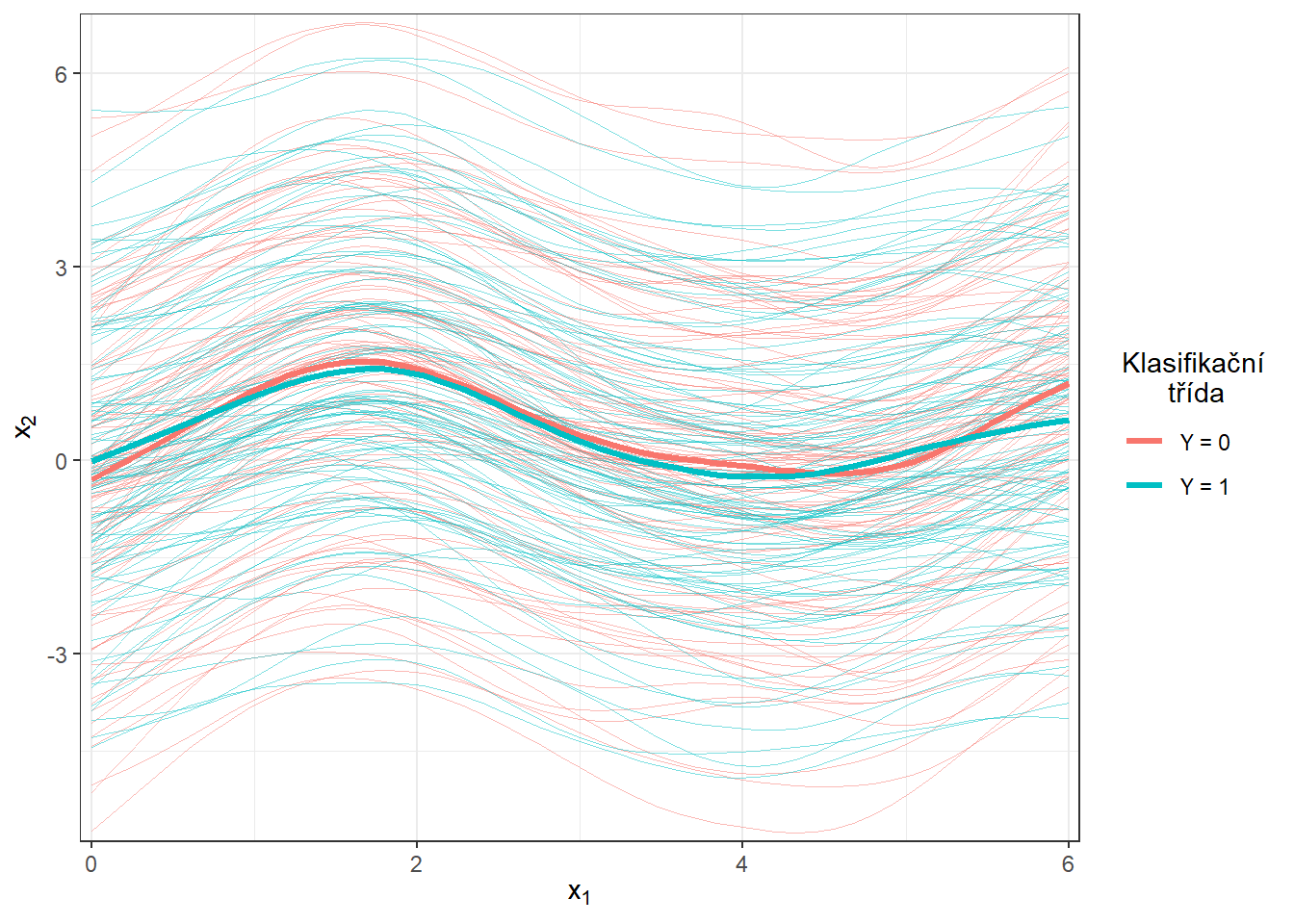

Obrázek 6.1: Vykreslení všech vyhlazených pozorovaných křivek, barevně jsou odlišeny křivky podle příslušnosti do klasifikační třídy. Tlustou čarou je zakreslen průměr pro každou třídu.

Code

DFsmooth <- data.frame(
  t = rep(t, 2 * n),
  time = rep(rep(1:n, each = length(t)), 2),
  Smooth = c(fdobjSmootheval),
  Mean = c(rep(apply(fdobjSmootheval[ , 1 : n], 1, mean), n),
            rep(apply(fdobjSmootheval[ , (n + 1) : (2 * n)], 1, mean), n)),
  group = factor(rep(c(0, 1), each = n * length(t)))
)

DFmean <- data.frame(
  t = rep(t, 2),
  Mean = c(apply(fdobjSmootheval[ , 1 : n], 1, mean), 
            apply(fdobjSmootheval[ , (n + 1) : (2 * n)], 1, mean)),
  group = factor(rep(c(0, 1), each = length(t)))
)

DFsmooth |> ggplot(aes(x = t, y = Smooth, group = interaction(time, group), 
                 colour = group)) + 
  geom_line(linewidth = 0.25, alpha = 0.5) +
  theme_bw() +
  labs(x = expression(x[1]),
       y = expression(x[2]),
       colour = 'Klasifikační\n      třída') +
  scale_colour_discrete(labels = c('Y = 0', 'Y = 1')) + 
  geom_line(aes(x = t, y = Mean, colour = group), 
            linewidth = 1.2, linetype = 'solid') + 
  scale_x_continuous(expand = c(0.01, 0.01)) + 
  #ylim(c(-1, 2)) + 
  scale_y_continuous(expand = c(0.01, 0.01), limits = c(-1, 2))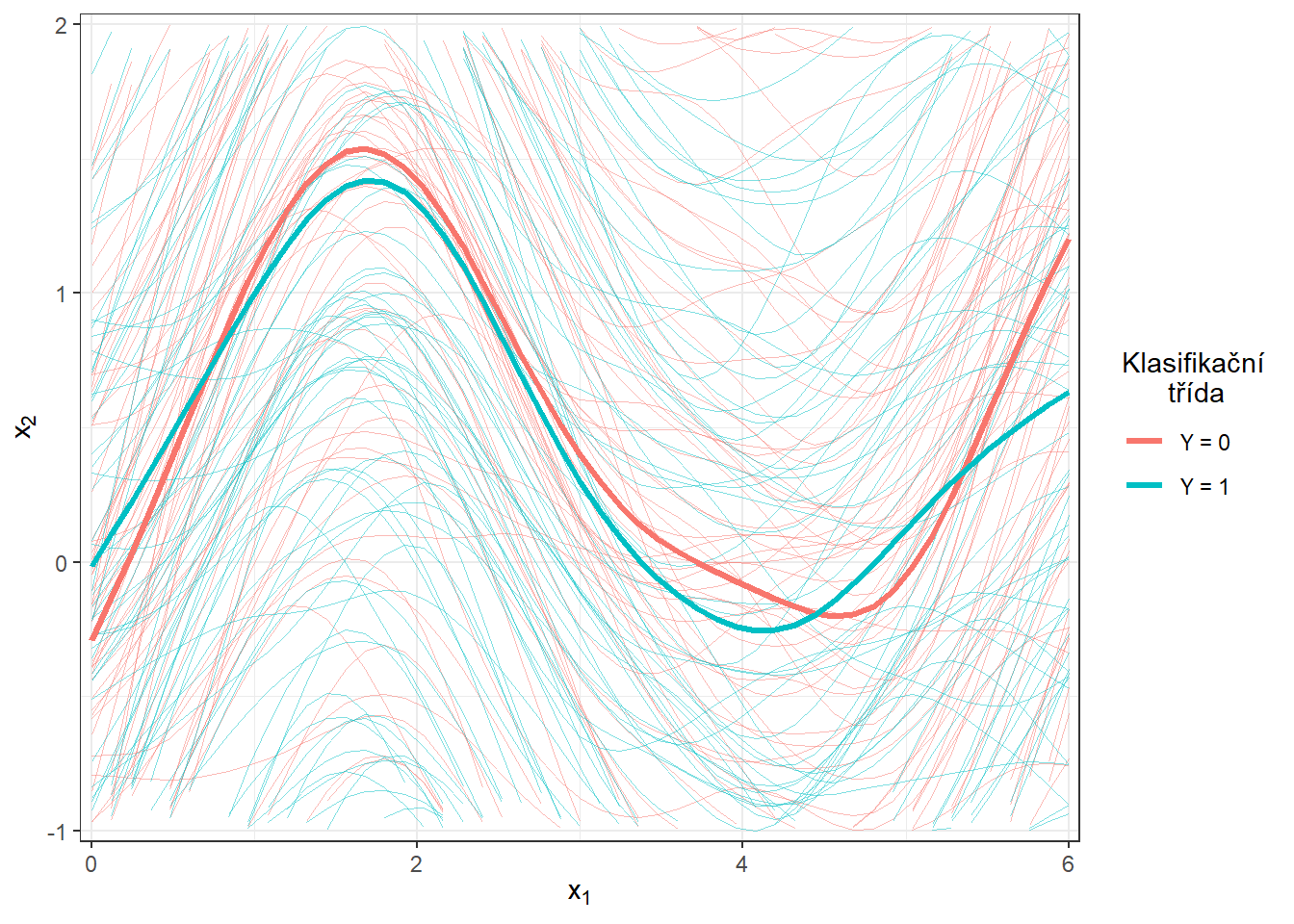

Obrázek 5.2: Vykreslení všech vyhlazených pozorovaných křivek, barevně jsou odlišeny křivky podle příslušnosti do klasifikační třídy. Tlustou čarou je zakreslen průměr pro každou třídu. Přiblížený pohled.

8.3 Klasifikace křivek

Nejprve načteme potřebné knihovny pro klasifikaci.

Code

library(caTools) # pro rozdeleni na testovaci a trenovaci
library(caret) # pro k-fold CV
library(fda.usc) # pro KNN, fLR
library(MASS) # pro LDA
library(fdapace)
library(pracma)
library(refund) # pro LR na skorech
library(nnet) # pro LR na skorech
library(caret)
library(rpart) # stromy
library(rattle) # grafika
library(e1071)
library(randomForest) # nahodny les

Abychom mohli jednotlivé klasifikátory porovnat, rozdělíme množinu vygenerovaných pozorování na dvě části v poměru 70:30, a to na trénovací a testovací (validační) část. Trénovací část použijeme při konstrukci klasifikátoru a testovací na výpočet chyby klasifikace a případně dalších charakteristik našeho modelu. Výsledné klasifikátory podle těchto spočtených charakteristik můžeme následně porovnat mezi sebou z pohledu jejich úspěšnosti klasifikace.

Code

# rozdeleni na testovaci a trenovaci cast
split <- sample.split(XXfd$fdnames$reps, SplitRatio = 0.7)

Y <- rep(c(0, 1), each = n)

X.train <- subset(XXfd, split == TRUE)
X.test <- subset(XXfd, split == FALSE)

Y.train <- subset(Y, split == TRUE)
Y.test <- subset(Y, split == FALSE)

Ještě se podíváme na zastoupení jednotlivých skupin v testovací a trénovací části dat.

8.3.1 Rozhodovací stromy

Rozhodovací stromy jsou velmi oblíbeným nástrojem ke klasifikaci, avšak jako v případě některých předchozích metod nejsou přímo určeny pro funkcionální data. Existují však postupy, jak funkcionální objekty převést na mnohorozměrné a následně na ně aplikovat algoritmus rozhodovacích stromů. Můžeme uvažovat následující postupy:

• algoritmus sestrojený na bázových koeficientech,
• využití skórů hlavních komponent,
• použít diskretizaci intervalu a vyhodnotit funkci jen na nějaké konečné síti bodů.

My samozřejmě nyní zvolíme poslední možnost. Nejprve si musíme definovat body z intervalu \(I = [0, 6]\), ve kterých funkce vyhodnotíme. Následně vytvoříme objekt, ve kterém budou řádky představovat jednotlivé (diskretizované) funkce a sloupce časy. Nakonec připojíme sloupec \(Y\) s informací o příslušnosti do klasifikační třídy a totéž zopakujeme i pro testovací data.

Code

# posloupnost bodu, ve kterych funkce vyhodnotime
p <- 101
t.seq <- seq(0, 6, length = p)
   
grid.data <- eval.fd(fdobj = X.train, evalarg = t.seq)
grid.data <- as.data.frame(t(grid.data)) # transpozice kvuli funkcim v radku
grid.data$Y <- Y.train |> factor()

grid.data.test <- eval.fd(fdobj = X.test, evalarg = t.seq)
grid.data.test <- as.data.frame(t(grid.data.test))
grid.data.test$Y <- Y.test |> factor()

Nyní mážeme sestrojit rozhodovací strom, ve kterém budou jakožto prediktory vystupovat všechny časy z vektoru t.seq. Tato klasifikační není náchylná na multikolinearitu, tudíž se jí nemusíme zabývat. Jako metriku zvolíme přesnost.

Code

# sestrojeni modelu
start_time <- Sys.time()
clf.tree <- train(Y ~ ., data = grid.data, 
                 method = "rpart", 
                 trControl = trainControl(method = "CV", number = 10),
                 metric = "Accuracy")
end_time <- Sys.time()

# presnost na trenovacich datech
predictions.train <- predict(clf.tree, newdata = grid.data)
presnost.train <- table(Y.train, predictions.train) |>
  prop.table() |> diag() |> sum()
  
# presnost na testovacich datech
predictions.test <- predict(clf.tree, newdata = grid.data.test)
presnost.test <- table(Y.test, predictions.test) |>
  prop.table() |> diag() |> sum()

Chybovost klasifikátoru na testovacích datech je tedy 46.67 % a na trénovacích datech 33.57 %. Časovou náročnost spočítáme následovně.

Code

duration <- end_time - start_time
duration |> print()

## Time difference of 0.435359 secs

Graficky si rozhodovací strom můžeme vykreslit pomocí funkce fancyRpartPlot(). Nastavíme barvy uzlů tak, aby reflektovaly předchozí barevné odlišení. Jedná se o neprořezaný strom.

Code

colnames(grid.data) <- c(paste0('time:', t.seq), 'Y')
fancyRpartPlot(rpart(Y ~ ., data = grid.data, method = "class"),
               sub = '', palettes = c('Reds', 'Blues')) 

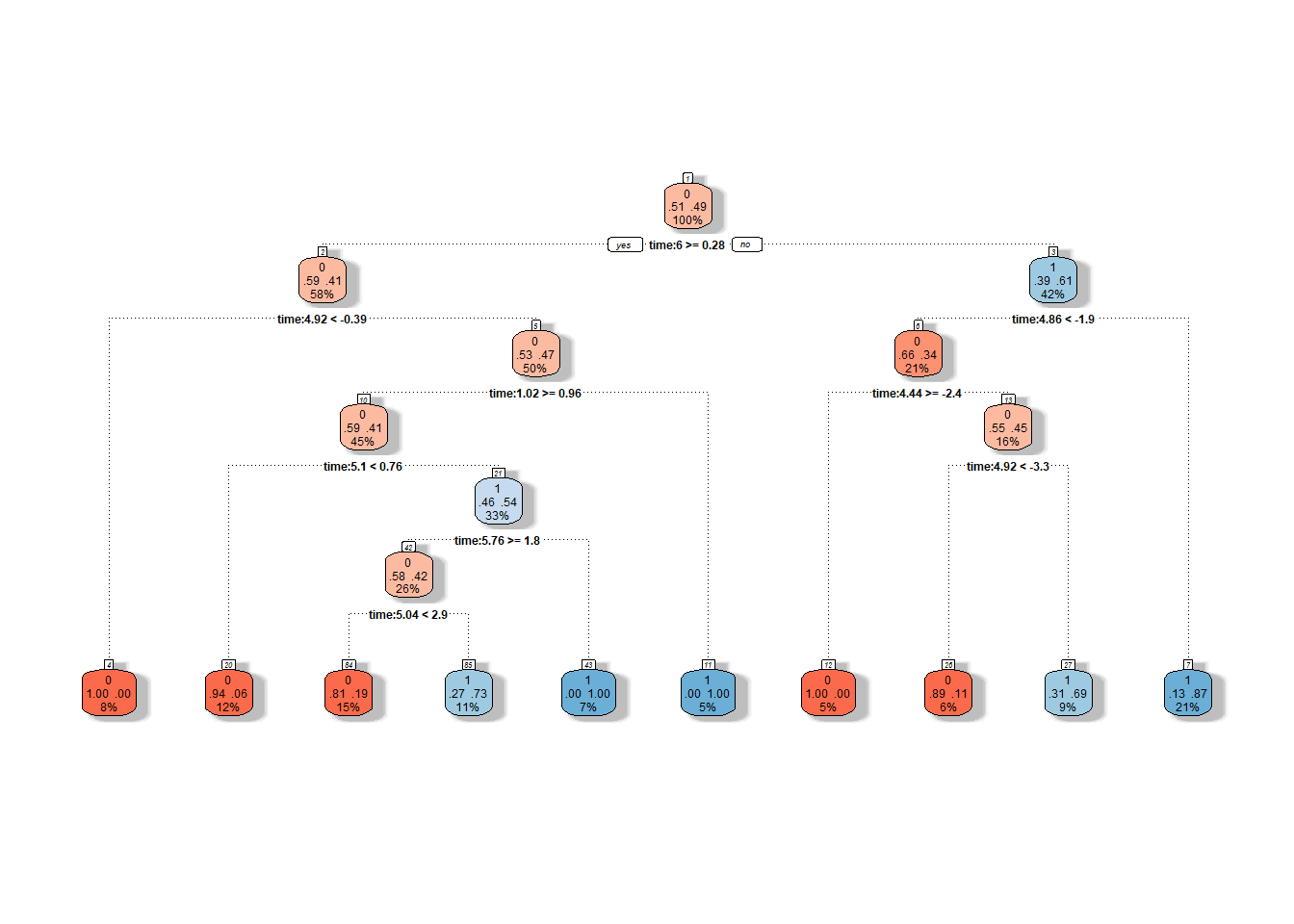
Obrázek 8.1: Grafické znázornění neprořezaného rozhodovacího stromu. Modrými odstíny jsou vykresleny uzly příslušející klasifikační třídě 1 a červenými odstíny třídě 0.

Můžeme si také vykreslit již prořezaný finální rozhodovací strom.

Code

rpart.plot::rpart.plot(clf.tree$finalModel, # finalni model ... prorezany strom
                       extra = 104, # zobrazeni pozadovanych informaci
                       box.palette = c('Reds', 'Blues'),
                       branch.lty = 3, # dotted branch lines
                       shadow.col = 0, # shadows under the node boxes
                       nn = FALSE, 
                       under = FALSE, 
                       digits = 2)

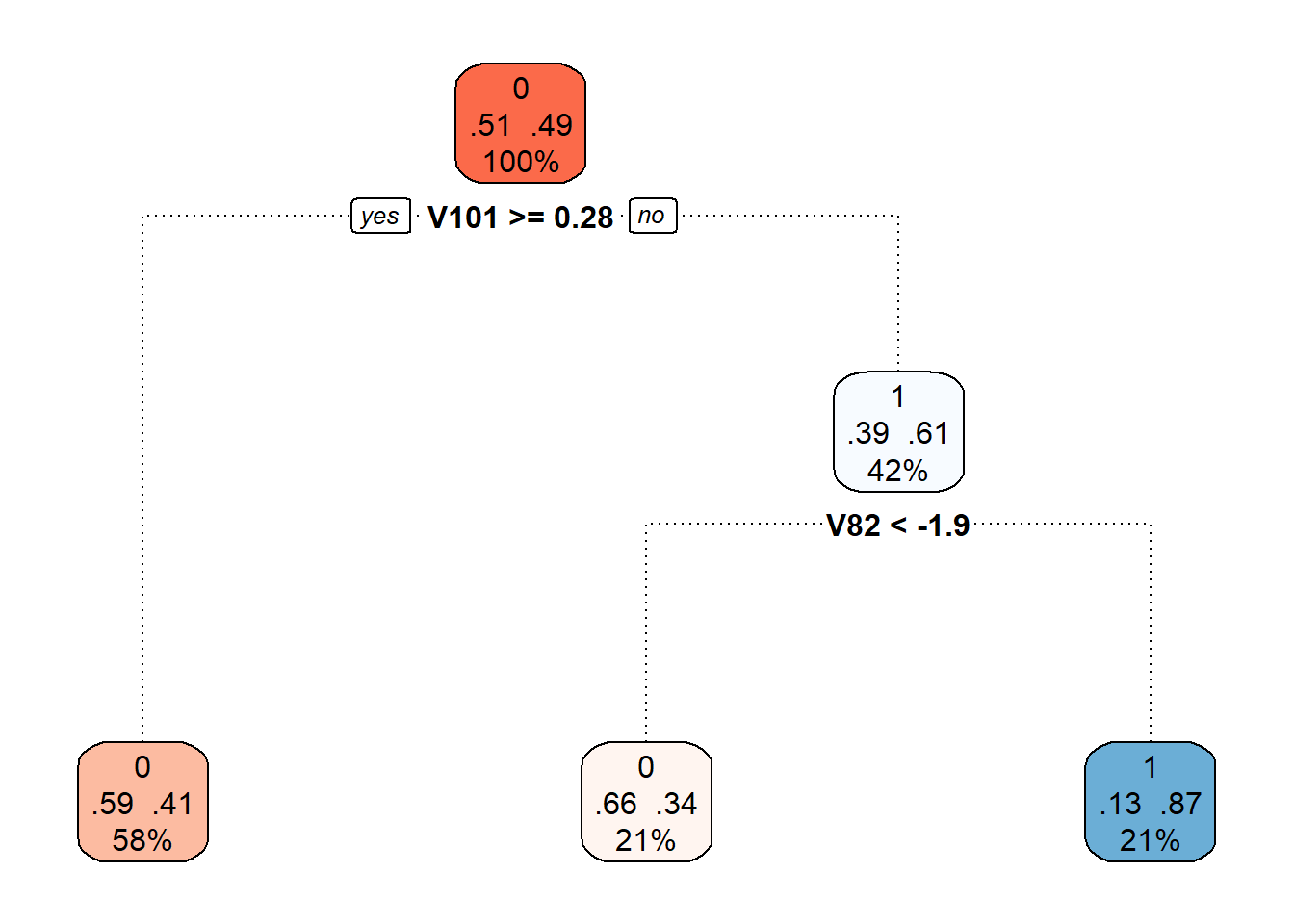
Obrázek 3.4: Finální prořezaný rozhodovací strom.

Nakonec opět přidejme trénovací a testovací chybovost do souhrnné tabulky.

Code

RESULTS <- data.frame(model = 'Tree - diskr.', 
                  Err.train = 1 - presnost.train,
                  Err.test = 1 - presnost.test,
                  Duration = as.numeric(duration))

8.3.2 Náhodné lesy

Klasifikátor sestrojený pomocí metody náhodných lesů spočívá v sestrojení několika jednotlivých rozhodovacích stromů, které se následně zkombinují a vytvoří společný klasifikátor (společným “hlasováním”).

Tak jako v případě rozhodovacích stromů máme několik možností na to, jaká data (konečně-rozměrná) použijeme pro sestrojení modelu. Budeme opět uvažovat diskretizaci intervalu. V tomto případě využíváme vyhodnocení funkcí na dané síti bodů intervalu \(I = [0, 6]\).

Code

# sestrojeni modelu
start_time <- Sys.time()
clf.RF <- randomForest(Y ~ ., data = grid.data, 
                       ntree = 500, # pocet stromu
                       importance = F,
                       nodesize = 1)
end_time <- Sys.time()

# presnost na trenovacich datech
predictions.train <- predict(clf.RF, newdata = grid.data)
presnost.train <- table(Y.train, predictions.train) |>
  prop.table() |> diag() |> sum()
  
# presnost na testovacich datech
predictions.test <- predict(clf.RF, newdata = grid.data.test)
presnost.test <- table(Y.test, predictions.test) |>
  prop.table() |> diag() |> sum()

Chybovost náhodného lesu na trénovacích datech je tedy 0 % a na testovacích datech 40 %. Časovou náročnost spočítáme následovně.

Code

duration <- end_time - start_time
duration |> print()

## Time difference of 0.343611 secs

Code

Res <- data.frame(model = 'RForest - diskr', 
                  Err.train = 1 - presnost.train,
                  Err.test = 1 - presnost.test,
                  Duration = as.numeric(duration))

RESULTS <- rbind(RESULTS, Res)

8.3.3 Support Vector Machines

Nyní se podívejme na klasifikaci našich nasimulovaných křivek pomocí metody podpůrných vektorů (ang. Support Vector Machines, SVM). Výhodou této klasifikační metody je její výpočetní nenáročnost, neboť pro definici hraniční křivky mezi třídami využívá pouze několik (často málo) pozorování.

V případě funkcionálních dat máme několik možností, jak použít metodu SVM. Nejjednodušší variantou je použít tuto klasifikační metodu přímo na diskretizovanou funkci. Začněme nejprve aplikací metody podpůrných vektorů přímo na diskretizovaná data (vyhodnocení funkce na dané síti bodů na intervalu \(I = [0, 6]\)), přičemž budeme uvažovat všech tři výše zmíněné jádrové funkce. Nejprve však data znormujeme.

Code

# set norm equal to one
norms <- c()
for (i in 1:dim(XXfd$coefs)[2]) {
  norms <- c(norms, as.numeric(1 / norm.fd(XXfd[i])))
  }
XXfd_norm <- XXfd 
XXfd_norm$coefs <- XXfd_norm$coefs * matrix(norms, 
                                            ncol = dim(XXfd$coefs)[2],
                                            nrow = dim(XXfd$coefs)[1],
                                            byrow = T)

# rozdeleni na testovaci a trenovaci cast
X.train_norm <- subset(XXfd_norm, split == TRUE)
X.test_norm <- subset(XXfd_norm, split == FALSE)

Y.train_norm <- subset(Y, split == TRUE)
Y.test_norm <- subset(Y, split == FALSE)

grid.data <- eval.fd(fdobj = X.train_norm, evalarg = t.seq)
grid.data <- as.data.frame(t(grid.data)) 
grid.data$Y <- Y.train_norm |> factor()

grid.data.test <- eval.fd(fdobj = X.test_norm, evalarg = t.seq)
grid.data.test <- as.data.frame(t(grid.data.test))
grid.data.test$Y <- Y.test_norm |> factor()

Code

# sestrojeni modelu
start_time <- Sys.time()
clf.SVM.l <- svm(Y ~ ., data = grid.data,
                 type = 'C-classification',
                 scale = TRUE,
                 cost = 100,
                 kernel = 'linear')
end_time <- Sys.time()

duration.l <- end_time - start_time

start_time <- Sys.time()
clf.SVM.p <- svm(Y ~ ., data = grid.data,
                 type = 'C-classification',
                 scale = TRUE,
                 coef0 = 1,
                 cost = 100,
                 kernel = 'polynomial')
end_time <- Sys.time()

duration.p <- end_time - start_time

start_time <- Sys.time()
clf.SVM.r <- svm(Y ~ ., data = grid.data,
                 type = 'C-classification',
                 scale = TRUE,
                 cost = 100000,
                 gamma = 0.0001,
                 kernel = 'radial')
end_time <- Sys.time()

duration.r <- end_time - start_time

# presnost na trenovacich datech
predictions.train.l <- predict(clf.SVM.l, newdata = grid.data)
presnost.train.l <- table(Y.train, predictions.train.l) |>
  prop.table() |> diag() |> sum()

predictions.train.p <- predict(clf.SVM.p, newdata = grid.data)
presnost.train.p <- table(Y.train, predictions.train.p) |>
  prop.table() |> diag() |> sum()

predictions.train.r <- predict(clf.SVM.r, newdata = grid.data)
presnost.train.r <- table(Y.train, predictions.train.r) |>
  prop.table() |> diag() |> sum()

# presnost na testovacich datech
predictions.test.l <- predict(clf.SVM.l, newdata = grid.data.test)
presnost.test.l <- table(Y.test, predictions.test.l) |>
  prop.table() |> diag() |> sum()

predictions.test.p <- predict(clf.SVM.p, newdata = grid.data.test)
presnost.test.p <- table(Y.test, predictions.test.p) |>
  prop.table() |> diag() |> sum()

predictions.test.r <- predict(clf.SVM.r, newdata = grid.data.test)
presnost.test.r <- table(Y.test, predictions.test.r) |>
  prop.table() |> diag() |> sum()

Chybovost metody SVM na trénovacích datech je tedy 5.71 % pro lineární jádro, 2.14 % pro polynomiální jádro a 3.57 % pro gaussovské jádro. Na testovacích datech je potom chybovost metody 16.67 % pro lineární jádro, 16.67 % pro polynomiální jádro a 13.33 % pro radiální jádro. Časovou náročnost spočítáme následovně.

Code

print('Linear kernel:', quote = F)

## [1] Linear kernel:

Code

duration.l |> print()

## Time difference of 0.02797294 secs

Code

print('Polynomial kernel:', quote = F)

## [1] Polynomial kernel:

Code

duration.p |> print()

## Time difference of 0.01821589 secs

Code

print('Radial kernel:', quote = F)

## [1] Radial kernel:

Code

duration.r |> print()

## Time difference of 0.0297451 secs

Code

Res <- data.frame(model = c('SVM linear - diskr', 
                            'SVM poly - diskr', 
                            'SVM rbf - diskr'), 
                  Err.train = 1 - c(presnost.train.l, presnost.train.p, presnost.train.r),
                  Err.test = 1 - c(presnost.test.l, presnost.test.p, presnost.test.r),
                  Duration = c(as.numeric(duration.l), 
                               as.numeric(duration.p), as.numeric(duration.r)))

RESULTS <- rbind(RESULTS, Res)

8.3.4 Tabulka výsledků

Tabulka 8.1: Souhrnné výsledky použitých metod na simulovaných datech. \(\widehat{Err}_{train}\) značí odhad trénovací chybovosti a \(\widehat{Err}_{test}\) testovací chybovosti.

Model	\(\widehat{Err}_{train}\quad\quad\quad\quad\quad\)	\(\widehat{Err}_{test}\quad\quad\quad\quad\quad\)	Duration
Tree - diskr.	0.3357	0.4667	0.4354
RForest - diskr	0.0000	0.4000	0.3436
SVM linear - diskr	0.0571	0.1667	0.0280
SVM poly - diskr	0.0214	0.1667	0.0182
SVM rbf - diskr	0.0357	0.1333	0.0297

8.4 Simulační studie

V celé předchozí části jsme se zabývali pouze jedním náhodně vygenerovaným souborem funkcí ze dvou klasifikačních tříd, který jsme následně opět náhodně rozdělili na testovací a trénovací část. Poté jsme jednotlivé klasifikátory získané pomocí uvažovaných metod ohodnotili na základě testovací a trénovací chybovosti.

Jelikož se vygenerovaná data (a jejich rozdělení na dvě části) mohou při každém zopakování výrazně lišit, budou se i chybovosti jednotlivých klasifikačních algoritmů výrazně lišit. Proto dělat jakékoli závěry o metodách a porovnávat je mezi sebou může být na základě jednoho vygenerovaného datového souboru velmi zavádějící.

Z tohoto důvodu se v této části zaměříme na opakování celého předchozího postupu pro různé vygenerované soubory. Výsledky si budeme ukládat do tabulky a nakonec spočítáme průměrné charakteristiky modelů přes jednotlivá opakování. Aby byly naše závěry dostatečně obecné, zvolíme počet opakování \(n_{sim} = 50\).

Nyní zopakujeme celou předchozí část n.sim-krát a hodnoty chybovostí si budeme ukládat to objektu SIMUL_params. Přitom budeme měnit hodnotu parametru \(p\) a podíváme se, jak se mění výsledky jednotlivých vybraných klasifikačních metod v závislosti na této hodnotě.

Code

# nastaveni generatoru pseudonahodnych cisel
set.seed(42)

# pocet simulaci pro kazdou hodnotu simulacniho parametru
n.sim <- 50

methods <- c('RF_discr',
             'SVM linear - diskr', 'SVM poly - diskr', 'SVM rbf - diskr')

# vektor delek p ekvidistantni posloupnosti 
p_vector <- seq(4, 250, by = 2)
# p_vector <- seq(10, 250, by = 10)

# vysledny objekt, do nehoz ukladame vysledky simulaci
SIMUL_params <- array(data = NA, dim = c(length(methods), 6, length(p_vector)),
                      dimnames = list(
                        method = methods,
                        metric = c('ERRtrain', 'Errtest', 
                                   'SDtrain', 'SDtest', 'Duration', 'SDduration'),
                        sigma = paste0(p_vector)))

# CV_res <- data.frame(matrix(NA, ncol = 4, 
#                             nrow = length(p_vector),
#                             dimnames = list(paste0(p_vector),
#                                             c('C.l', 'C.p', 'C.r', 'gamma'))))

for (n_p in 1:length(p_vector)) {
  ## list, do ktereho budeme ukladat hodnoty chybovosti
  # ve sloupcich budou metody
  # v radcich budou jednotliva opakovani
  # list ma dve polozky ... train a test
  SIMULACE <- list(train = as.data.frame(matrix(NA, ncol = length(methods), 
                                               nrow = n.sim,
                                               dimnames = list(1:n.sim, methods))), 
                   test = as.data.frame(matrix(NA, ncol = length(methods), 
                                               nrow = n.sim,
                                               dimnames = list(1:n.sim, methods))),
                   duration = as.data.frame(matrix(NA, ncol = length(methods), 
                                               nrow = n.sim,
                                               dimnames = list(1:n.sim, methods)))#,
                   # CV = as.data.frame(matrix(NA, ncol = 4, 
                   #                             nrow = n.sim,
                   #                             dimnames = list(1:n.sim, 
                   #                                             c('C.l', 'C.p', 'C.r', 'gamma'))))
                   )
  
  ## SIMULACE
  
  for(sim in 1:n.sim) {
    # pocet vygenerovanych pozorovani pro kazdou tridu
    n <- 100
    # vektor casu ekvidistantni na intervalu [0, 6]
    t <- seq(0, 6, length = 51)
    
    # pro Y = 0
    X0 <- generate_values(t, funkce_0, n, 1, 2)
    # pro Y = 1
    X1 <- generate_values(t, funkce_1, n, 1, 2)
    
    rangeval <- range(t)
    breaks <- t
    norder <- 4
    
    bbasis <- create.bspline.basis(rangeval = rangeval, 
                                   norder = norder, 
                                   breaks = breaks)
    
    curv.Lfd <- int2Lfd(2) 
    # spojeni pozorovani do jedne matice
    XX <- cbind(X0, X1)
    
    lambda.vect <- 10^seq(from = -4, to = 2, length.out = 40) # vektor lambd
    gcv <- rep(NA, length = length(lambda.vect)) # prazdny vektor pro ulozebi GCV
    
    for(index in 1:length(lambda.vect)) {
      curv.Fdpar <- fdPar(bbasis, curv.Lfd, lambda.vect[index])
      BSmooth <- smooth.basis(t, XX, curv.Fdpar) # vyhlazeni
      gcv[index] <- mean(BSmooth$gcv) # prumer pres vsechny pozorovane krivky
    }
    
    GCV <- data.frame(
      lambda = round(log10(lambda.vect), 3),
      GCV = gcv
    )
    
    # najdeme hodnotu minima
    lambda.opt <- lambda.vect[which.min(gcv)]
    
    curv.fdPar <- fdPar(bbasis, curv.Lfd, lambda.opt)
    BSmooth <- smooth.basis(t, XX, curv.fdPar)
    XXfd <- BSmooth$fd
    
    fdobjSmootheval <- eval.fd(fdobj = XXfd, evalarg = t)
    
    # rozdeleni na testovaci a trenovaci cast
    split <- sample.split(XXfd$fdnames$reps, SplitRatio = 0.7)
    
    Y <- rep(c(0, 1), each = n)
    
    X.train <- subset(XXfd, split == TRUE)
    X.test <- subset(XXfd, split == FALSE)
    
    Y.train <- subset(Y, split == TRUE)
    Y.test <- subset(Y, split == FALSE)
    
    x.train <- fdata(X.train)
    y.train <- as.numeric(factor(Y.train))
    
    ## 1) Rozhodovací stromy
    
    # posloupnost bodu, ve kterych funkce vyhodnotime
    t.seq <- seq(0, 6, length = p_vector[n_p])
       
    grid.data <- eval.fd(fdobj = X.train, evalarg = t.seq)
    grid.data <- as.data.frame(t(grid.data)) # transpozice kvuli funkcim v radku
    grid.data$Y <- Y.train |> factor()
    
    grid.data.test <- eval.fd(fdobj = X.test, evalarg = t.seq)
    grid.data.test <- as.data.frame(t(grid.data.test))
    grid.data.test$Y <- Y.test |> factor()
    
    # sestrojeni modelu
    # start_time <- Sys.time()
    # clf.tree <- train(Y ~ ., data = grid.data, 
    #                  method = "rpart", 
    #                  trControl = trainControl(method = "CV", number = 10),
    #                  metric = "Accuracy")
    # end_time <- Sys.time()
    # duration <- end_time - start_time
    # 
    # # presnost na trenovacich datech
    # predictions.train <- predict(clf.tree, newdata = grid.data)
    # presnost.train <- table(Y.train, predictions.train) |>
    #   prop.table() |> diag() |> sum()
    #   
    # # presnost na trenovacich datech
    # predictions.test <- predict(clf.tree, newdata = grid.data.test)
    # presnost.test <- table(Y.test, predictions.test) |>
    #   prop.table() |> diag() |> sum()
    # 
    # RESULTS <- data.frame(model = 'Tree_discr', 
    #                   Err.train = 1 - presnost.train,
    #                   Err.test = 1 - presnost.test,
    #                   Duration = as.numeric(duration))
    
    ## 2) Náhodné lesy
  
    # sestrojeni modelu
    start_time <- Sys.time()
    clf.RF <- randomForest(Y ~ ., data = grid.data, 
                           ntree = 500, # pocet stromu
                           importance = TRUE,
                           nodesize = 5)
    end_time <- Sys.time()
    duration <- end_time - start_time
    
    # presnost na trenovacich datech
    predictions.train <- predict(clf.RF, newdata = grid.data)
    presnost.train <- table(Y.train, predictions.train) |>
      prop.table() |> diag() |> sum()
      
    # presnost na trenovacich datech
    predictions.test <- predict(clf.RF, newdata = grid.data.test)
    presnost.test <- table(Y.test, predictions.test) |>
      prop.table() |> diag() |> sum()
    
    RESULTS <- data.frame(model = 'RF_discr', 
                      Err.train = 1 - presnost.train,
                      Err.test = 1 - presnost.test,
                      Duration = as.numeric(duration))
    
    # RESULTS <- rbind(RESULTS, Res)
    
    ## 3) SVM
    
    # normovani dat
    norms <- c()
    for (i in 1:dim(XXfd$coefs)[2]) {
      norms <- c(norms, as.numeric(1 / norm.fd(XXfd[i])))
      }
    XXfd_norm <- XXfd 
    XXfd_norm$coefs <- XXfd_norm$coefs * matrix(norms, 
                                                ncol = dim(XXfd$coefs)[2],
                                                nrow = dim(XXfd$coefs)[1],
                                                byrow = T)
    
    # rozdeleni na testovaci a trenovaci cast
    X.train_norm <- subset(XXfd_norm, split == TRUE)
    X.test_norm <- subset(XXfd_norm, split == FALSE)
    
    Y.train_norm <- subset(Y, split == TRUE)
    Y.test_norm <- subset(Y, split == FALSE)
    
    grid.data <- eval.fd(fdobj = X.train_norm, evalarg = t.seq)
    grid.data <- as.data.frame(t(grid.data)) 
    grid.data$Y <- Y.train_norm |> factor()
    
    grid.data.test <- eval.fd(fdobj = X.test_norm, evalarg = t.seq)
    grid.data.test <- as.data.frame(t(grid.data.test))
    grid.data.test$Y <- Y.test_norm |> factor()
    
    start_time <- Sys.time()
    clf.SVM.l <- svm(Y ~ ., data = grid.data,
                     type = 'C-classification',
                     scale = TRUE,
                     cost = 100,
                     kernel = 'linear')
    end_time <- Sys.time()

    duration.l <- end_time - start_time

    start_time <- Sys.time()
    clf.SVM.p <- svm(Y ~ ., data = grid.data,
                     type = 'C-classification',
                     scale = TRUE,
                     coef0 = 1,
                     cost = 100,
                     kernel = 'polynomial')
    end_time <- Sys.time()

    duration.p <- end_time - start_time

    start_time <- Sys.time()
    clf.SVM.r <- svm(Y ~ ., data = grid.data,
                     type = 'C-classification',
                     scale = TRUE,
                     cost = 100000,
                     gamma = 0.0001,
                     kernel = 'radial')
    end_time <- Sys.time()

    duration.r <- end_time - start_time

    # presnost na trenovacich datech
    predictions.train.l <- predict(clf.SVM.l, newdata = grid.data)
    presnost.train.l <- table(Y.train, predictions.train.l) |>
      prop.table() |> diag() |> sum()

    predictions.train.p <- predict(clf.SVM.p, newdata = grid.data)
    presnost.train.p <- table(Y.train, predictions.train.p) |>
      prop.table() |> diag() |> sum()

    predictions.train.r <- predict(clf.SVM.r, newdata = grid.data)
    presnost.train.r <- table(Y.train, predictions.train.r) |>
      prop.table() |> diag() |> sum()

    # presnost na testovacich datech
    predictions.test.l <- predict(clf.SVM.l, newdata = grid.data.test)
    presnost.test.l <- table(Y.test, predictions.test.l) |>
      prop.table() |> diag() |> sum()

    predictions.test.p <- predict(clf.SVM.p, newdata = grid.data.test)
    presnost.test.p <- table(Y.test, predictions.test.p) |>
      prop.table() |> diag() |> sum()

    predictions.test.r <- predict(clf.SVM.r, newdata = grid.data.test)
    presnost.test.r <- table(Y.test, predictions.test.r) |>
      prop.table() |> diag() |> sum()
    
    # # rozdelime trenovaci data na k casti
    # k_cv <- 5
    # folds <- createMultiFolds(1:sum(split), k = k_cv, time = 1)
    # # kontrola, ze mame opravdu k = k_cv
    # while (length(folds) != k_cv) {
    #   folds <- createMultiFolds(1:sum(split), k = k_cv, time = 1)
    # }
    # 
    # # ktere hodnoty gamma chceme uvazovat
    # gamma.cv <- 10^seq(-4, 3, length = 8)
    # C.cv <- 10^seq(-3, 5, length = 9)
    # p.cv <- 3
    # coef0 <- 1
    # 
    # # list se tremi slozkami ... array pro jednotlive jadra -> linear, poly, radial
    # # prazdna matice, do ktere vlozime jednotlive vysledky
    # # ve sloupcich budou hodnoty presnosti pro dane
    # # v radcich budou hodnoty pro danou gamma a vrstvy odpovidaji folds
    # CV.results <- list(
    #   SVM.l = array(NA, dim = c(length(C.cv), k_cv)),
    #   SVM.p = array(NA, dim = c(length(C.cv), length(p.cv), k_cv)),
    #   SVM.r = array(NA, dim = c(length(C.cv), length(gamma.cv), k_cv))
    # )
    # 
    # # nejprve projdeme hodnoty C
    # for (C in C.cv) {
    #   # projdeme jednotlive folds
    #   for (index_cv in 1:k_cv) {
    #     # definice testovaci a trenovaci casti pro CV
    #     fold <- folds[[index_cv]]
    #     cv_sample <- 1:dim(grid.data)[1] %in% fold
    #     
    #     data.grid.train.cv <- as.data.frame(grid.data[cv_sample, ])
    #     data.grid.test.cv <- as.data.frame(grid.data[!cv_sample, ])
    #     
    #     ## LINEARNI JADRO
    #     # sestrojeni modelu
    #     clf.SVM.l <- svm(Y ~ ., data = data.grid.train.cv,
    #                      type = 'C-classification',
    #                      scale = TRUE,
    #                      cost = C,
    #                      kernel = 'linear')
    #     
    #     # presnost na validacnich datech
    #     predictions.test.l <- predict(clf.SVM.l, newdata = data.grid.test.cv)
    #     presnost.test.l <- table(data.grid.test.cv$Y, predictions.test.l) |>
    #       prop.table() |> diag() |> sum()
    #     
    #     # presnosti vlozime na pozice pro dane C a fold
    #     CV.results$SVM.l[(1:length(C.cv))[C.cv == C], 
    #                      index_cv] <- presnost.test.l
    #     
    #     ## POLYNOMIALNI JADRO
    #     for (p in p.cv) {
    #       # sestrojeni modelu
    #       clf.SVM.p <- svm(Y ~ ., data = data.grid.train.cv,
    #                        type = 'C-classification',
    #                        scale = TRUE,
    #                        cost = C,
    #                        coef0 = 1,
    #                        degree = p,
    #                        kernel = 'polynomial')
    #       
    #       # presnost na validacnich datech
    #       predictions.test.p <- predict(clf.SVM.p, 
    #                                     newdata = data.grid.test.cv)
    #       presnost.test.p <- table(data.grid.test.cv$Y, predictions.test.p) |>
    #         prop.table() |> diag() |> sum()
    #       
    #       # presnosti vlozime na pozice pro dane C, p a fold
    #       CV.results$SVM.p[(1:length(C.cv))[C.cv == C], 
    #                        (1:length(p.cv))[p.cv == p],
    #                        index_cv] <- presnost.test.p
    #     }
    #         
    #     ## RADIALNI JADRO
    #     for (gamma in gamma.cv) {
    #       # sestrojeni modelu
    #       clf.SVM.r <- svm(Y ~ ., data = data.grid.train.cv,
    #                        type = 'C-classification',
    #                        scale = TRUE,
    #                        cost = C,
    #                        gamma = gamma,
    #                        kernel = 'radial')
    #       
    #       # presnost na validacnich datech
    #       predictions.test.r <- predict(clf.SVM.r, newdata = data.grid.test.cv)
    #       presnost.test.r <- table(data.grid.test.cv$Y, predictions.test.r) |>
    #         prop.table() |> diag() |> sum()
    #       
    #       # presnosti vlozime na pozice pro dane C, gamma a fold
    #       CV.results$SVM.r[(1:length(C.cv))[C.cv == C], 
    #                        (1:length(gamma.cv))[gamma.cv == gamma],
    #                        index_cv] <- presnost.test.r
    #     }
    #   }
    # }
    # # spocitame prumerne presnosti pro jednotliva C pres folds
    # ## Linearni jadro
    # CV.results$SVM.l <- apply(CV.results$SVM.l, 1, mean)
    # ## Polynomialni jadro
    # CV.results$SVM.p <- apply(CV.results$SVM.p, c(1, 2), mean)
    # ## Radialni jadro
    # CV.results$SVM.r <- apply(CV.results$SVM.r, c(1, 2), mean)
    # 
    # C.opt <- c(which.max(CV.results$SVM.l), 
    #            which.max(CV.results$SVM.p) %% length(C.cv), 
    #            which.max(CV.results$SVM.r) %% length(C.cv))
    # C.opt[C.opt == 0] <- length(C.cv)
    # C.opt <- C.cv[C.opt]
    # 
    # gamma.opt <- which.max(t(CV.results$SVM.r)) %% length(gamma.cv)
    # gamma.opt[gamma.opt == 0] <- length(gamma.cv)
    # gamma.opt <- gamma.cv[gamma.opt]
    # 
    # SIMULACE$CV[sim, ] <- c(C.opt, gamma.opt)
    # 
    # # sestrojeni modelu
    # start_time <- Sys.time()
    # clf.SVM.l <- svm(Y ~ ., data = grid.data,
    #                  type = 'C-classification',
    #                  scale = TRUE,
    #                  cost = C.opt[1],
    #                  kernel = 'linear')
    # end_time <- Sys.time()
    # 
    # duration.l <- end_time - start_time
    # 
    # start_time <- Sys.time()
    # clf.SVM.p <- svm(Y ~ ., data = grid.data,
    #                  type = 'C-classification',
    #                  scale = TRUE,
    #                  cost = C.opt[2],
    #                  degree = p.opt,
    #                  coef0 = 1,
    #                  kernel = 'polynomial')
    # end_time <- Sys.time()
    # 
    # duration.p <- end_time - start_time
    # 
    # start_time <- Sys.time()
    # clf.SVM.r <- svm(Y ~ ., data = grid.data,
    #                  type = 'C-classification',
    #                  scale = TRUE, 
    #                  cost = C.opt[3],
    #                  gamma = gamma.opt,
    #                  kernel = 'radial')
    # end_time <- Sys.time()
    # 
    # duration.r <- end_time - start_time
    # 
    # # presnost na trenovacich datech
    # predictions.train.l <- predict(clf.SVM.l, newdata = grid.data)
    # presnost.train.l <- table(Y.train, predictions.train.l) |>
    #   prop.table() |> diag() |> sum()
    # 
    # predictions.train.p <- predict(clf.SVM.p, newdata = grid.data)
    # presnost.train.p <- table(Y.train, predictions.train.p) |>
    #   prop.table() |> diag() |> sum()
    # 
    # predictions.train.r <- predict(clf.SVM.r, newdata = grid.data)
    # presnost.train.r <- table(Y.train, predictions.train.r) |>
    #   prop.table() |> diag() |> sum()
    # 
    # # presnost na testovacich datech
    # predictions.test.l <- predict(clf.SVM.l, newdata = grid.data.test)
    # presnost.test.l <- table(Y.test, predictions.test.l) |>
    #   prop.table() |> diag() |> sum()
    # 
    # predictions.test.p <- predict(clf.SVM.p, newdata = grid.data.test)
    # presnost.test.p <- table(Y.test, predictions.test.p) |>
    #   prop.table() |> diag() |> sum()
    # 
    # predictions.test.r <- predict(clf.SVM.r, newdata = grid.data.test)
    # presnost.test.r <- table(Y.test, predictions.test.r) |>
    #   prop.table() |> diag() |> sum()
    
    Res <- data.frame(model = c('SVM linear - diskr', 
                                'SVM poly - diskr', 
                                'SVM rbf - diskr'), 
                      Err.train = 1 - c(presnost.train.l,
                                        presnost.train.p, presnost.train.r),
                      Err.test = 1 - c(presnost.test.l, 
                                       presnost.test.p, presnost.test.r),
                      Duration = c(as.numeric(duration.l), 
                               as.numeric(duration.p), as.numeric(duration.r)))
    
    RESULTS <- rbind(RESULTS, Res)

    ## pridame vysledky do objektu SIMULACE
    
    SIMULACE$train[sim, ] <- RESULTS$Err.train
    SIMULACE$test[sim, ] <- RESULTS$Err.test
    SIMULACE$duration[sim, ] <- RESULTS$Duration
    cat('\r', paste0(n_p, ': ', sim))
  }
  
  # Nyní spočítáme průměrné testovací a trénovací chybovosti pro jednotlivé 
  # klasifikační metody.
  
  # dame do vysledne tabulky
  
  SIMULACE.df <- data.frame(Err.train = apply(SIMULACE$train, 2, mean),
                            Err.test = apply(SIMULACE$test, 2, mean),
                            SD.train = apply(SIMULACE$train, 2, sd),
                            SD.test = apply(SIMULACE$test, 2, sd),
                            Duration = apply(SIMULACE$duration, 2, mean),
                            SD.dur = apply(SIMULACE$duration, 2, sd))
  
  # CV_res[n_p, ] <- apply(SIMULACE$CV, 2, median)
  
  SIMUL_params[, , n_p] <- as.matrix(SIMULACE.df)
}

# ulozime vysledne hodnoty 
save(SIMUL_params, file = 'RData/simulace_params_diskretizace_03_cv.RData')

8.4.1 Grafický výstup

Podívejme se na závislost simulovaných výsledků na hodnotě parametru \(p\). Začněme trénovacími chybovostmi.

Code

methods_names <- c(
      # 'Rozhodovací strom',
      'Náhodný les',
      'SVM (linear)',
      'SVM (poly)',
      'SVM (radial)'
)

Code

# pro trenovaci data
SIMUL_params[, 1, ] |> 
  as.data.frame() |> 
  mutate(method = methods) |>
  pivot_longer(cols = as.character(p_vector), 
               names_to = 'p', 
               values_to = 'Err') |>
  mutate(method = factor(method, levels = methods, labels = methods, ordered = TRUE), 
         p = as.numeric(p)) |> 
  filter(method %in% c("RF_discr", "SVM linear - diskr",
                       "SVM poly - diskr", "SVM rbf - diskr")) |>
  ggplot(aes(x = p, y = Err, colour = method)) + 
  geom_line() + 
  theme_bw() + 
  labs(x = expression(p),
       y = expression(widehat(Err)[train]),
       colour = 'Klasifikační metoda') + 
  theme(legend.position = 'right')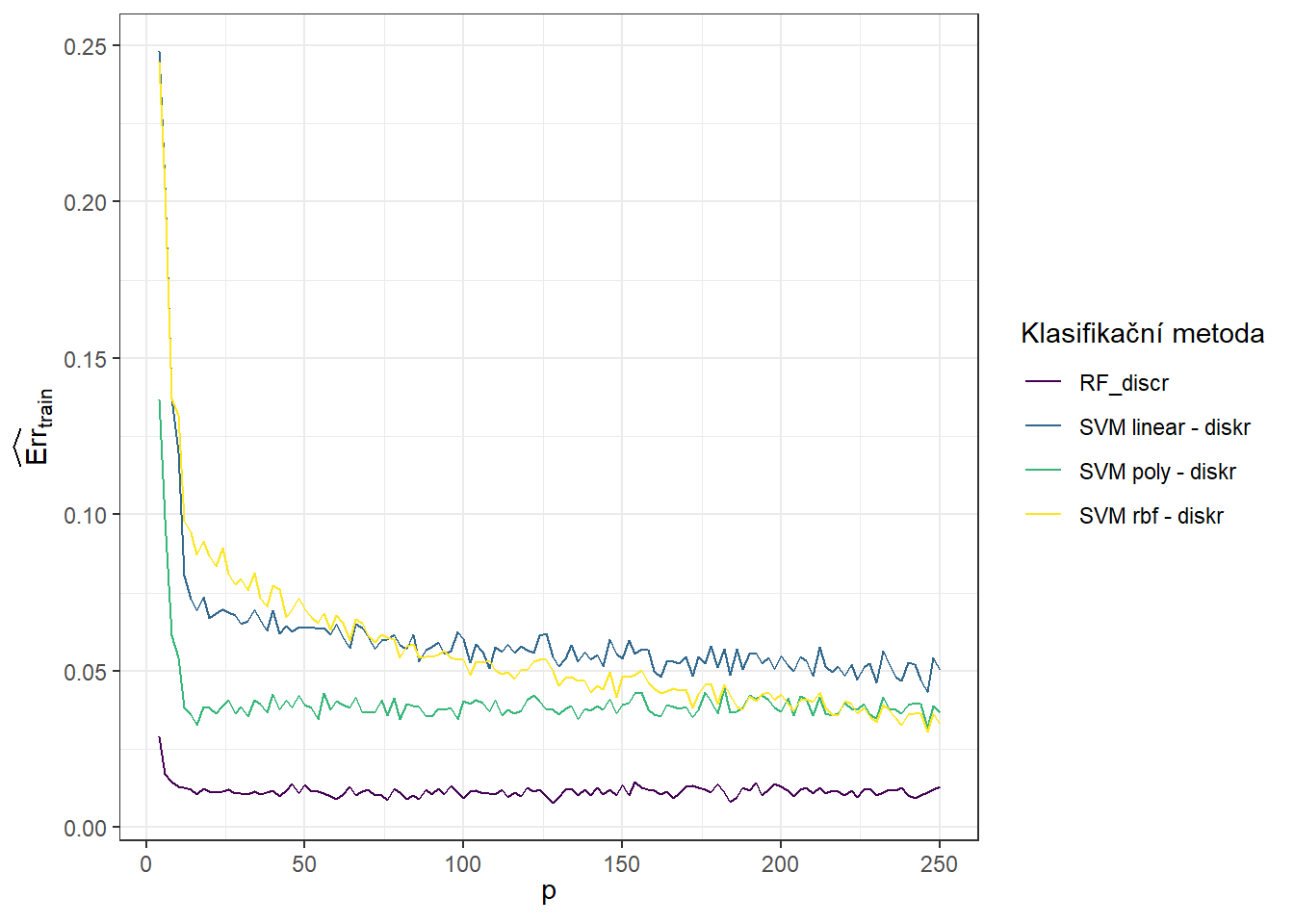

Obrázek 1.12: Graf závislosti trénovací chybovosti pro jednotlivé klasifikační metody na hodnotě parametru \(p\).

Následně pro testovací chybovosti, což je graf, který nás zajímá nejvíce.

Code

# pro testovaci data
SIMUL_params[, 2, ] |> 
  as.data.frame() |> 
  mutate(method = methods) |>
  pivot_longer(cols = as.character(p_vector), 
               names_to = 'p', 
               values_to = 'Err') |>
  mutate(method = factor(method, levels = methods, labels = methods, ordered = TRUE), 
         p = as.numeric(p)) |> 
  filter(method %in% c("RF_discr", "SVM linear - diskr",
                       "SVM poly - diskr", "SVM rbf - diskr")) |>
  ggplot(aes(x = p, y = Err, colour = method)) + 
  geom_line() + 
  theme_bw() + 
  labs(x = expression(p),
       y = expression(widehat(Err)[test]),
       colour = 'Klasifikační metoda') + 
  theme(legend.position = 'right')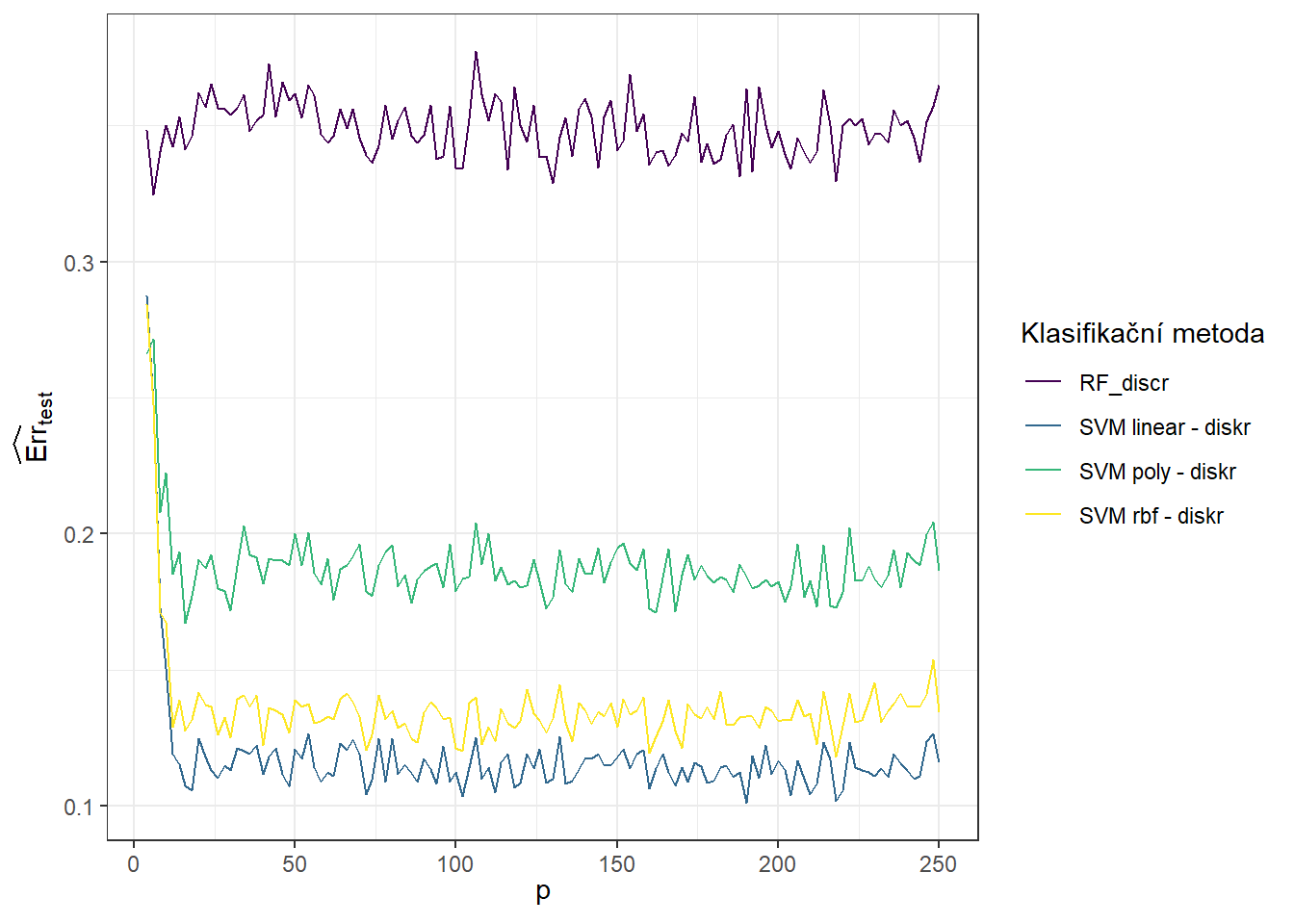

Obrázek 1.13: Graf závislosti testovací chybovosti pro jednotlivé klasifikační metody na hodnotě parametru \(p\).

Nakonec si vykresleme graf pro časovou náročnost metod.

Code

SIMUL_params[, 5, ] |> 
  as.data.frame() |> 
  mutate(method = methods) |>
  pivot_longer(cols = as.character(p_vector), 
               names_to = 'p', 
               values_to = 'Duration') |>
  mutate(method = factor(method, levels = methods, labels = methods, ordered = TRUE), 
         p = as.numeric(p)) |> 
  filter(method %in% c("RF_discr", "SVM linear - diskr",
                       "SVM poly - diskr", "SVM rbf - diskr")) |>
  ggplot(aes(x = p, y = Duration, colour = method, linetype = method)) + 
  geom_line() + 
  theme_bw() + 
  labs(x = expression(p),
       y = "Duration [s]",
       colour = 'Klasifikační metoda',
       linetype = 'Klasifikační metoda') + 
  theme(legend.position = 'right') + 
  scale_y_log10() +
  scale_colour_manual(values = c('deepskyblue2', 'deepskyblue2', 'tomato',
                                 'tomato', 'tomato')) + 
  scale_linetype_manual(values = c('solid', 'dashed',
                                   'solid', 'dashed', 'dotted'))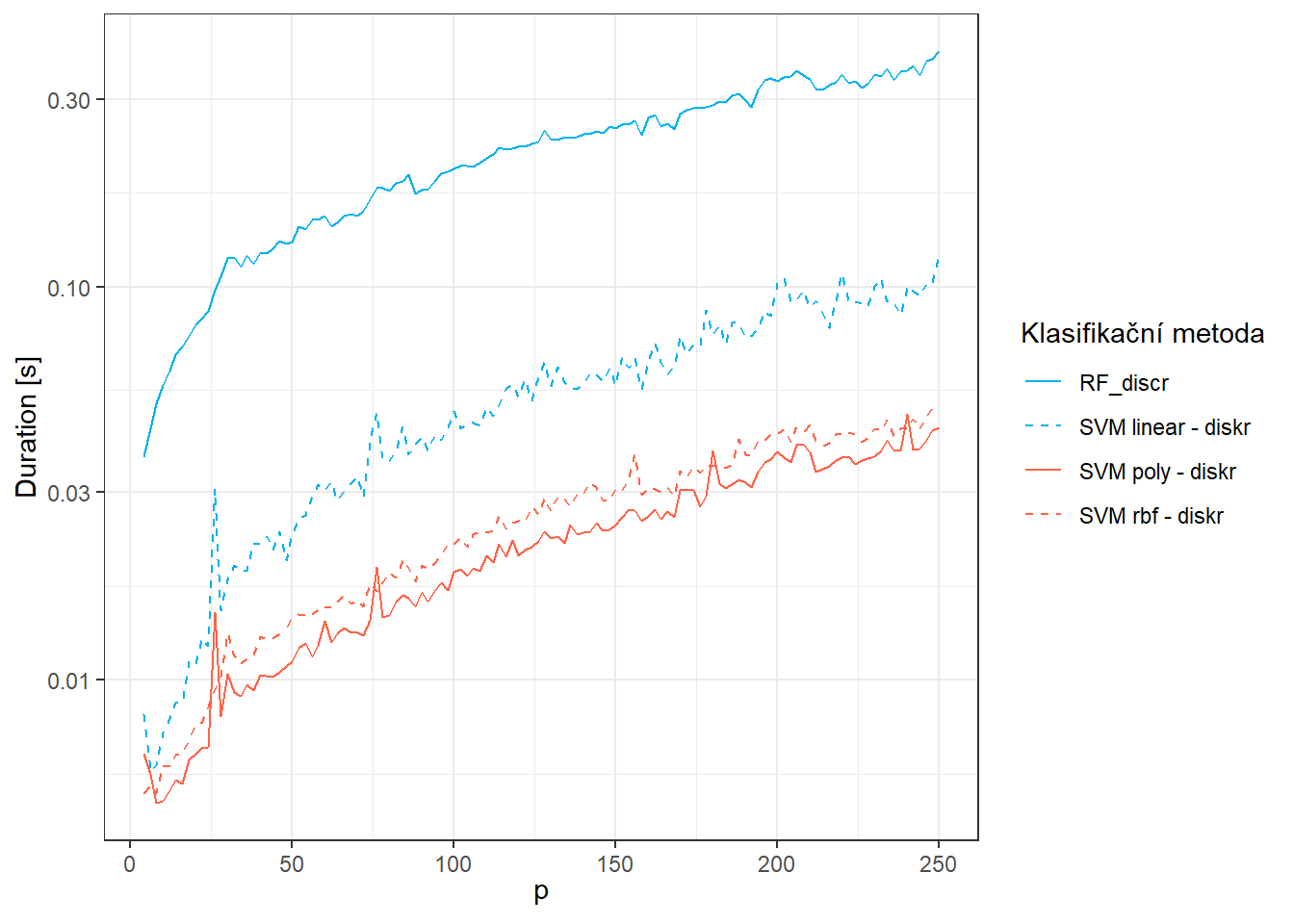

Obrázek 7.4: Graf závislosti časové náročnosti metod pro jednotlivé klasifikační metody na hodnotě parametru \(p\).

Jelikož jsou výsledky zatíženy náhodnými výchylkami a zvýšení počtu opakování n.sim by bylo výpočetně velmi náročné, vyhlaďme nyní křivky závislosti průměrné testovací chybovosti na počtu \(p\).

Code

Dat <- SIMUL_params[, 2, ] |> 
  as.data.frame() |> t()

breaks <- p_vector
rangeval <- range(breaks)
norder <- 4
wtvec <- rep(1, 124)
# wtvec <- c(seq(50, 10, length = 4), seq(0.1, 0.1, length = 10), rep(1, 110))

bbasis <- create.bspline.basis(rangeval = rangeval, 
                               norder = norder, 
                               breaks = breaks)

curv.Lfd <- int2Lfd(2)

lambda.vect <- 10^seq(from = 3, to = 5, length.out = 50) # vektor lambd
gcv <- rep(NA, length = length(lambda.vect)) # prazdny vektor pro ulozebi GCV

for(index in 1:length(lambda.vect)) {
  curv.Fdpar <- fdPar(bbasis, curv.Lfd, lambda.vect[index])
  BSmooth <- smooth.basis(breaks, Dat, curv.Fdpar, 
                          wtvec = wtvec) # vyhlazeni
  gcv[index] <- mean(BSmooth$gcv) # prumer pres vsechny pozorovane krivky
}

GCV <- data.frame(
  lambda = round(log10(lambda.vect), 3),
  GCV = gcv
)

# najdeme hodnotu minima
lambda.opt <- lambda.vect[which.min(gcv)]

curv.fdPar <- fdPar(bbasis, curv.Lfd, lambda.opt)
BSmooth <- smooth.basis(breaks, Dat, curv.fdPar,
                        wtvec = wtvec)
XXfd <- BSmooth$fd

fdobjSmootheval <- eval.fd(fdobj = XXfd, 
                           evalarg = seq(min(p_vector), max(p_vector), length = 101))

df_plot_smooth <- data.frame(
  method = rep(colnames(fdobjSmootheval), each = dim(fdobjSmootheval)[1]),
  value = c(fdobjSmootheval),
  p = rep(seq(min(p_vector), max(p_vector), length = 101), length(methods))
) |> 
  mutate(method = factor(method, levels = methods, labels = methods, ordered = TRUE))

Code

# pro testovaci data
p1 <- SIMUL_params[, 2, ] |> 
  as.data.frame() |> 
  mutate(method = methods) |>
  pivot_longer(cols = as.character(p_vector), 
               names_to = 'p', 
               values_to = 'Err') |>
  mutate(method = factor(method, levels = methods, labels = methods, ordered = TRUE), 
         p = as.numeric(p)) |> 
  filter(method %in% c("RF_discr", "SVM linear - diskr",
                       "SVM poly - diskr", "SVM rbf - diskr")) |>
  ggplot(aes(x = p, y = Err, colour = method, shape = method)) + 
  geom_point(alpha = 0.7, size = 0.6) + 
  theme_bw() + 
  labs(x = 'p',
       y = 'Testovaci chybovost',
       colour = 'Klasifikační metoda',
       linetype = 'Klasifikační metoda',
       shape = 'Klasifikační metoda') + 
  theme(legend.position = 'none',
        plot.margin = unit(c(0.1, 0.1, 0.3, 0.5), "cm"),
        panel.grid.minor.x = element_blank()) +
    # scale_y_log10() +
  geom_line(data = df_plot_smooth, aes(x = p, y = value, col = method,
                                       linetype = method),
            linewidth = 0.95) + 
  scale_colour_manual(values = c('deepskyblue2', 'deepskyblue2', #'tomato',
                                 'tomato', 'tomato'),
                      labels = methods_names) + 
  scale_linetype_manual(values = c('solid', 'dashed',
                                   'solid', 'dashed'#, 'dotted'
                                   ),
                        labels = methods_names) + 
  scale_shape_manual(values = c(16, 1, 16, 1),
                     labels = methods_names) +
  guides(colour = guide_legend(override.aes = list(size = 1.2, alpha = 0.7)),
         linetype = guide_legend(override.aes = list(linewidth = 0.8)))
p1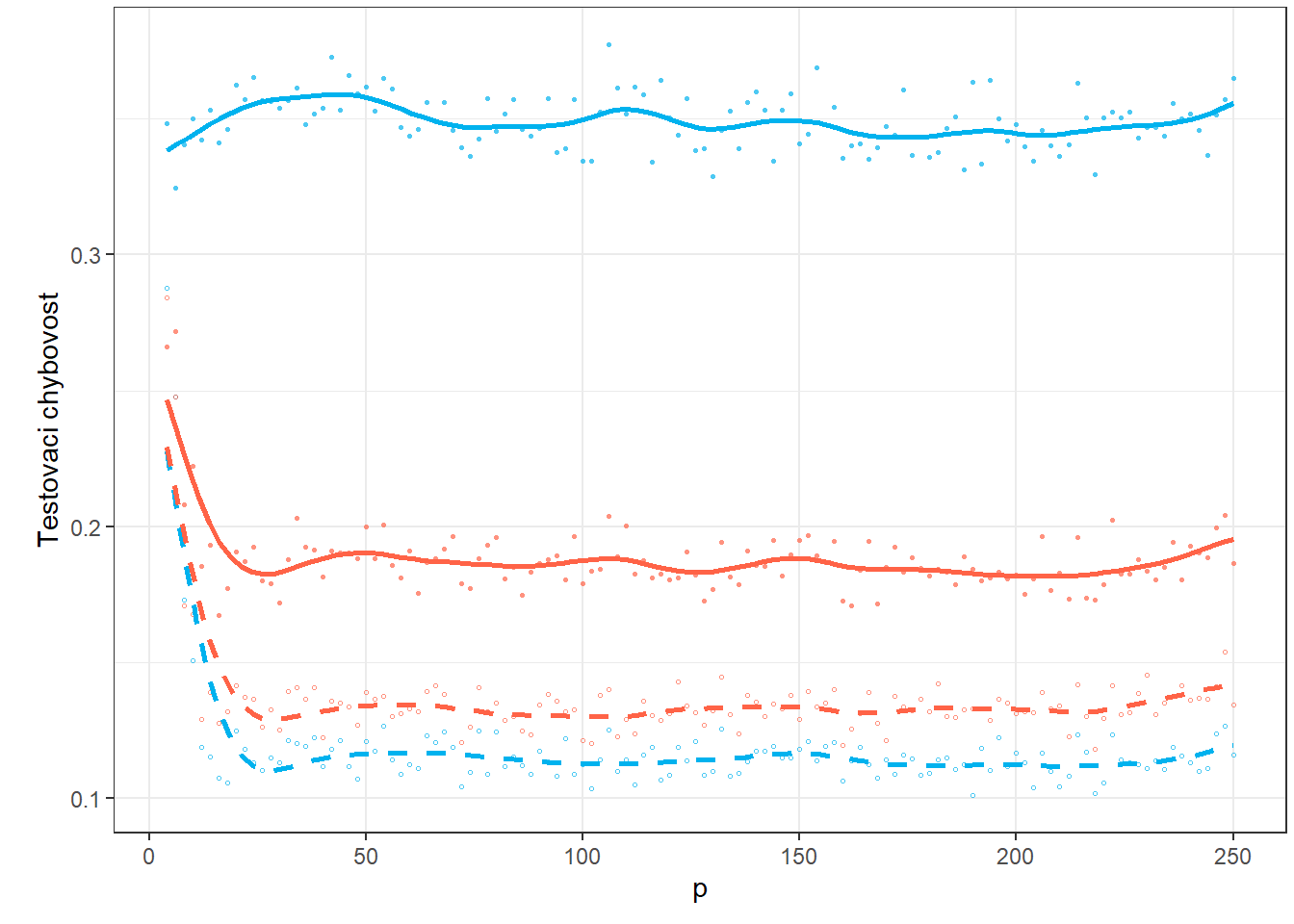

Obrázek 2.7: Graf závislosti testovací chybovosti pro jednotlivé klasifikační metody na hodnotě parametru \(p\).

Code

# ggsave("figures/kap6_sim_03diskr_curvesErr.tex", device = tikz, width = 4.5, height = 4.5)

Přidáme ke grafu časovou náročnost.

Code

Dat <- SIMUL_params[, 5, ] |> 
  as.data.frame() |> t()

breaks <- p_vector
rangeval <- range(breaks)
norder <- 4
wtvec <- rep(1, 124)
# wtvec <- c(seq(50, 10, length = 4), seq(0.1, 0.1, length = 10), rep(1, 110))

bbasis <- create.bspline.basis(rangeval = rangeval, 
                               norder = norder, 
                               breaks = breaks)

curv.Lfd <- int2Lfd(2)

lambda.vect <- 10^seq(from = 3, to = 5, length.out = 50) # vektor lambd
gcv <- rep(NA, length = length(lambda.vect)) # prazdny vektor pro ulozebi GCV

for(index in 1:length(lambda.vect)) {
  curv.Fdpar <- fdPar(bbasis, curv.Lfd, lambda.vect[index])
  BSmooth <- smooth.basis(breaks, Dat, curv.Fdpar, 
                          wtvec = wtvec) # vyhlazeni
  gcv[index] <- mean(BSmooth$gcv) # prumer pres vsechny pozorovane krivky
}

GCV <- data.frame(
  lambda = round(log10(lambda.vect), 3),
  GCV = gcv
)

# najdeme hodnotu minima
lambda.opt <- lambda.vect[which.min(gcv)]

curv.fdPar <- fdPar(bbasis, curv.Lfd, lambda.opt)
BSmooth <- smooth.basis(breaks, Dat, curv.fdPar,
                        wtvec = wtvec)
XXfd <- BSmooth$fd

fdobjSmootheval <- eval.fd(fdobj = XXfd, 
                           evalarg = seq(min(p_vector), max(p_vector), length = 101))

df_plot_smooth_2 <- data.frame(
  method = rep(colnames(fdobjSmootheval), each = dim(fdobjSmootheval)[1]),
  value = c(fdobjSmootheval),
  p = rep(seq(min(p_vector), max(p_vector), length = 101), length(methods))
) |> 
  mutate(method = factor(method, levels = methods, labels = methods, ordered = TRUE))

Code

# pro testovaci data
p2 <- SIMUL_params[, 5, ] |> 
  as.data.frame() |> 
  mutate(method = methods) |>
  pivot_longer(cols = as.character(p_vector), 
               names_to = 'p', 
               values_to = 'Err') |>
  mutate(method = factor(method, levels = methods, labels = methods, ordered = TRUE), 
         p = as.numeric(p)) |> 
  filter(method %in% c("RF_discr", "SVM linear - diskr",
                       "SVM poly - diskr", "SVM rbf - diskr")) |>
  ggplot(aes(x = p, y = Err, colour = method, shape = method)) + 
  geom_point(alpha = 0.7, size = 0.6) + 
  theme_bw() + 
  labs(x = 'p',
       y = 'Testovaci chybovost',
       colour = 'Klasifikační metoda',
       linetype = 'Klasifikační metoda',
       shape = 'Klasifikační metoda') + 
  theme(legend.position = c(0.7, 0.16),#'right',
        plot.margin = unit(c(0.1, 0.1, 0.3, 0.5), "cm"),
        panel.grid.minor = element_blank(),
        legend.background = element_rect(fill='transparent'),
        legend.key = element_rect(colour = NA, fill = NA)) +
  scale_y_log10() +
  geom_line(data = df_plot_smooth_2, aes(x = p, y = value, col = method,
                                       linetype = method),
            linewidth = 0.95) + 
  scale_colour_manual(values = c('deepskyblue2', 'deepskyblue2', #'tomato',
                                 'tomato', 'tomato'),
                      labels = methods_names) + 
  scale_linetype_manual(values = c('solid', 'dashed',
                                   'solid', 'dashed'#, 'dotted'
                                   ),
                        labels = methods_names) + 
  scale_shape_manual(values = c(16, 1, 16, 1),
                     labels = methods_names) +
  guides(colour = guide_legend(override.aes = list(size = 1.2, alpha = 0.7)),
         linetype = guide_legend(override.aes = list(linewidth = 0.8)))
p2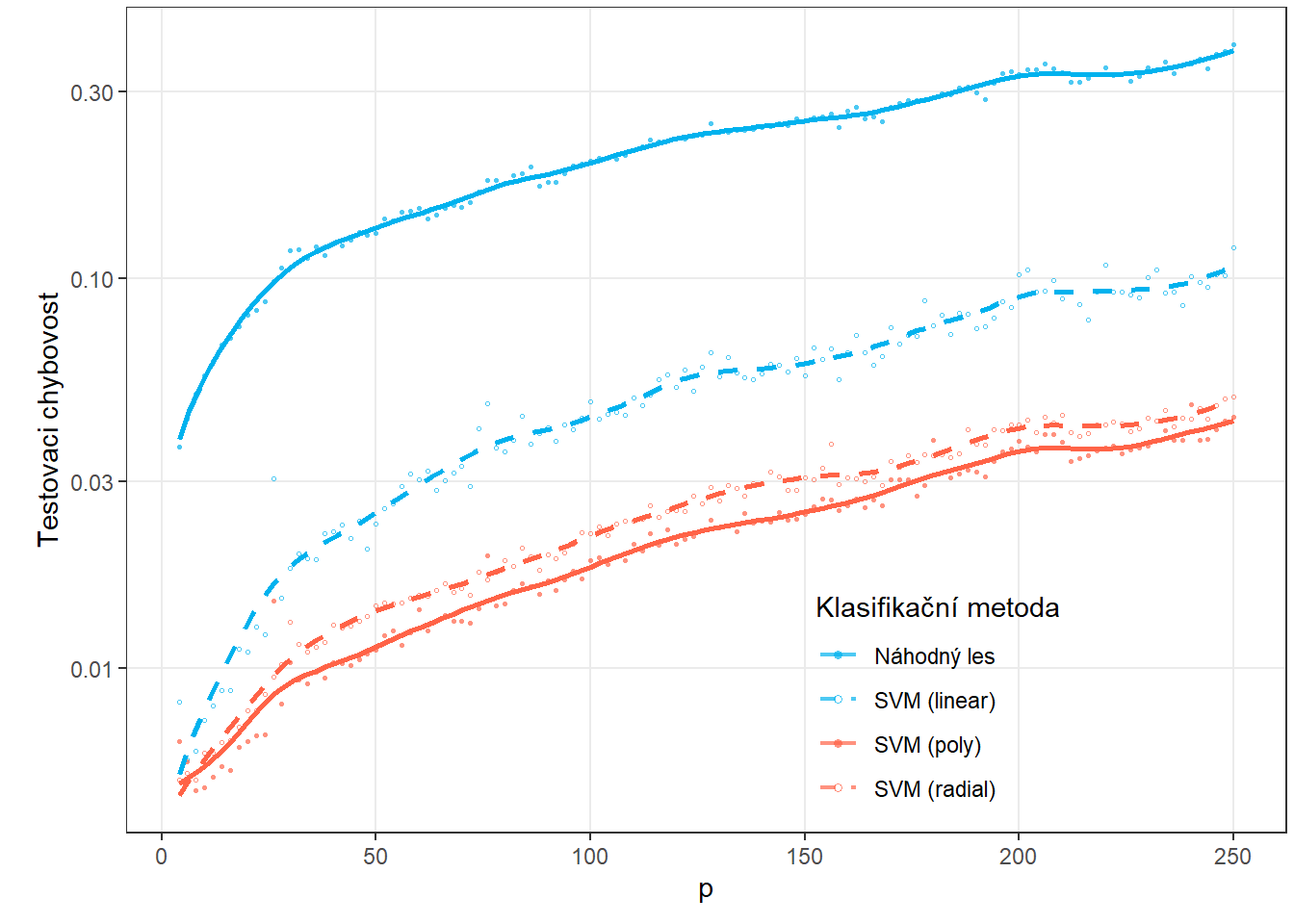

Obrázek 5.8: Graf závislosti testovací chybovosti pro jednotlivé klasifikační metody na hodnotě parametru \(p\).

Code

# ggsave("figures/kap6_sim_03diskr_curvesTime.tex", device = tikz, width = 4.5, height = 4.5)

Podrobné komentáře k výsledkům této simulační studie lze najít v diplomové práci.